题目内容
袋中有红、黄、白3种颜色的球各1只,从中每次任取1只,有放回地抽取3次,求:
(1)“3只球颜色全相同”的概率.
(2)“3只球颜色不全相同”的概率.
解 (1)“3只球颜色全相同”包括“3只全是红球”(事件A),“3只全是黄球”(事件B),“3只全是白球”(事件C),且它们彼此互斥,故“3只球颜色全相同”这个事件可记为A∪B∪C,又P(A)
=P(B)=P(C)= ,故P(A∪B∪C)
,故P(A∪B∪C)
=P(A)+P(B)+P(C)= .
.
(2)记“3只球颜色不全相同”为事件D,则事件 为“3只球颜色全相同”,
为“3只球颜色全相同”,
又P( )=P(A∪B∪C)=
)=P(A∪B∪C)= .
.
所以P(D)=1-P( )=1-
)=1- =
= ,
,
故“3只球颜色不全相同”的概率为 .
.

 阅读快车系列答案
阅读快车系列答案登山族为了了解某山高y(km)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
由表中数据,得到线性回归方程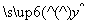 =-2x+
=-2x+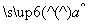 (
(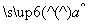 ∈R),由此请估计出山高为72(km)处气温的度数为( )
∈R),由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8
C.-4 D.-6
已知 的展开式中的常数项为T,f(x)是以T为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是________.
的展开式中的常数项为T,f(x)是以T为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是________.
从一堆苹果中任取了20个,并得到它们的质量(单位:克)数据分布表如下:
| 分组 | [90,100) | [100, 110) | [110, 120) | [120, 130) | [130, 140) | [140, 150] |
| 频数 | 1 | 2 | 3 | 10 | 3 | 1 |
则这堆苹果中质量不小于120克的苹果数约占苹果总数的________%.
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
其中健康指数的含义是:2表示“健康”,1表示“基本健康”,0表示“不健康,但生活能够自理”,-1表示“生活不能自理”.
(1)估计该地区80岁以下老龄人生活能够自理的概率;
(2)若一个地区老龄人健康指数的平均值不小于1.2,则该地区可被评为“老龄健康地区”.请写出该地区老龄人健康指数X的分布列,并判断该地区能否被评为“老龄健康地区”.
 B.
B.
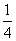 D.
D.
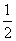 B.
B.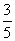
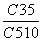 D.C
D.C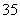 ·0.55
·0.55