题目内容
20.已知数列{an}的通项公式为an=|n-13|,那么满足a1+a2+…+ak=114的整数k的值是( )| A. | 20 | B. | 21 | C. | 23 | D. | 24 |
分析 根据数列的通项公式,去绝对值符号,因此对k进行讨论,进而求得a1+a2+…+ak的表达式,解方程即可求得结果.
解答 解:∵an=|n-13|=$\left\{\begin{array}{l}n-13,n≥13\\ 13-n,1≤n<13\end{array}\right.$,
∴a1+a2+…+ak=(13-1)+(13-2)+(13-3)+…+(13-13)+(14-13)+…+(k-13)=$\frac{13(0+12)}{2}$+$\frac{(k-13)(1+k-13)}{2}$=114,
解得k=21.
故选:B.
点评 本题考查根据数列的通项公式求数列的和,体现了分类讨论的数学思想,去绝对值是解题的关键,考查运算能力,属中档题.

练习册系列答案
相关题目
11.已知函数f(x)=x2-2|x-a|(a∈R).
(I)当a=0时,求方程f(x)=0的根;
(Ⅱ)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≥2f(x)恒成立,求实数a的取值范围.
(I)当a=0时,求方程f(x)=0的根;
(Ⅱ)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≥2f(x)恒成立,求实数a的取值范围.
8.函数$f(x)={x^2}(x-\frac{2}{x})$的导函数f′(x),则f′(1)等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
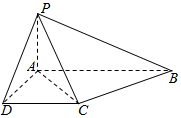 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求:
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求: