题目内容
方程log
x=2x-1的实数根的个数为（ ）
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、不确定 |
分析：将方程log
x=2x-1的实数根的个数转化成y=log
x与y=2x-1的图象的交点的个数，在同一坐标系下画出它们的图象，观察图象即可得到结论．
| 1 |
| 2 |
| 1 |
| 2 |
解答：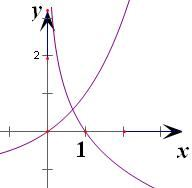
解：方程log
x=2x-1的实数根的个数可看成
y=log
x与y=2x-1的图象的交点的个数
在同一坐标系下画出它们的图象
显然一个交点，
故方程log
x=2x-1的实数根的个数为1
故选B．
解：方程log| 1 |
| 2 |
y=log
| 1 |
| 2 |
在同一坐标系下画出它们的图象
显然一个交点，
故方程log
| 1 |
| 2 |
故选B．
点评：本题主要考查了函数与方程的综合运用，以及指数函数与对数函数的图象，属于基础题．
练习册系列答案
相关题目
设x1、x2、x3依次是方程log
x+2=x，log2(x+2)=
，2x+x=2的实根，则x1、x2、x3的大小关系是（ ）
| 1 |
| 2 |
| -x |
| A、x1＜x2＜x3 |
| B、x2＜x3＜x1 |
| C、x1＜x3＜x2 |
| D、x3＜x2＜x1 |