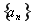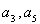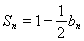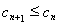题目内容
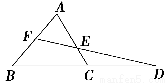
如图，在△ABC中，延长BC到D，使CD＝BC，取AB的中点F，连接FD交AC于点E.
(1)求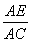
的值；
(2)若AB＝a，FB＝EC，求AC的长．
(1) 
(2) 
a
【解析】
解 (1)如图所示，过点F作FM∥AC，交BC于点M.
∵F为AB的中点，∴M为BC的中点，
∴FM＝
AC，由FM∥AC，
得∠CED＝∠MFD，∠ECD＝∠FMD.
∴△FMD∽△ECD.
∴
＝
＝
.
∴EC＝
FM＝
×
AC＝
AC，
∴
＝
＝.
(2)∵AB＝a，∴FB＝
AB＝
a.
又FB＝EC，∴EC＝
a.
∵EC＝
AC，∴AC＝3EC＝a.
练习册系列答案
相关题目
