题目内容
【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)设{an}的公差为d,
则a10=a1+9d=19, ![]() ,
,
解得a1=1,d=2,所以an=2n﹣1,)
所以b1b2b3…bn﹣1bn=2n+1…①
当n=1时,b1=3,
当n≥2时,b1b2b3…bn﹣1=2n﹣1…②
①②两式相除得 ![]()
因为当n=1时,b1=3适合上式,所以 ![]() .
.
(Ⅱ)由已知 ![]() ,
,
得 ![]()
则Tn=c1+c2+c3+…+cn= ![]() ,
,
当n为偶数时, ![]()
= ![]()
= ![]() ,
,
当n为奇数时, ![]()
= ![]()
= ![]() .
.
综上: 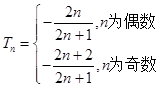
【解析】(Ⅰ)由题意和等差数列的前n项和公式求出公差,代入等差数列的通项公式化简求出an , 再化简b1b2b3…bn﹣1bn=an+2,可得当n≥2时b1b2b3…bn﹣1=2n﹣1,将两个式子相除求出bn;(Ⅱ)由(1)化简cn=(﹣1)n ![]() ,再对n分奇数和偶数讨论,分别利用裂项相消法求出Tn , 最后要用分段函数的形式表示出来.
,再对n分奇数和偶数讨论,分别利用裂项相消法求出Tn , 最后要用分段函数的形式表示出来.
【考点精析】解答此题的关键在于理解等差数列的前n项和公式的相关知识,掌握前n项和公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系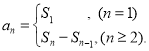 .
.

练习册系列答案
相关题目