题目内容
经过A(2,0),以(2cosθ-2,sinθ)为方向向量的直线与经过B(-2,0),以(2+2cosθ,sinθ)为方向向量的直线相交于点M(x,y),其中θ≠kπ。
(Ⅰ)求点M(x,y)的轨迹方程;
(Ⅱ)设(Ⅰ)中轨迹为曲线C,F1( ,0),F2(
,0),F2( ,0),若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求
,0),若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求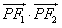 的取值范围。
的取值范围。
(Ⅰ)求点M(x,y)的轨迹方程;
(Ⅱ)设(Ⅰ)中轨迹为曲线C,F1(
 ,0),F2(
,0),F2( ,0),若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求
,0),若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求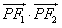 的取值范围。
的取值范围。 解:(Ⅰ) ,
,
∴ , ①
, ①
同理 ,②
,②
①×②得 ,
,
∴ 。
。
(Ⅱ)设 ,则
,则 , ③
, ③
∴ ,
,
化简,得 , ④
, ④
④代入③得, ,
,
∴ ,
,
化简,得 。
。
 ,
,∴
 , ①
, ①同理
 ,②
,②①×②得
 ,
,∴
 。
。(Ⅱ)设
 ,则
,则 , ③
, ③∴
 ,
,化简,得
 , ④
, ④④代入③得,
 ,
,∴
 ,
,化简,得
 。
。
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
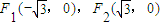 ,若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求
,若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求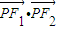 的取值范围.
的取值范围.