题目内容
已知定义在正实数集上的函数f(x)= x2+2ex,g(x)=3e2lnx+b(其中e为常数,e=2.718 28…),若这两个函数的图象有公共点,且在该点处的切线相同,
x2+2ex,g(x)=3e2lnx+b(其中e为常数,e=2.718 28…),若这两个函数的图象有公共点,且在该点处的切线相同,
(Ⅰ)求实数b的值;
(Ⅱ)当x∈[ ,e]时,
,e]时, 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
 x2+2ex,g(x)=3e2lnx+b(其中e为常数,e=2.718 28…),若这两个函数的图象有公共点,且在该点处的切线相同,
x2+2ex,g(x)=3e2lnx+b(其中e为常数,e=2.718 28…),若这两个函数的图象有公共点,且在该点处的切线相同,(Ⅰ)求实数b的值;
(Ⅱ)当x∈[
 ,e]时,
,e]时, 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。解:(Ⅰ)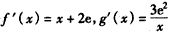 ,
,
设函数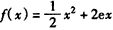 与
与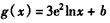 的图象有公共点为
的图象有公共点为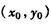 ,
,
由题意,得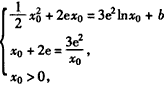 ,
,
解得: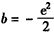 。
。
(Ⅱ)由(Ⅰ)知,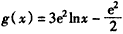 ,
,
所以,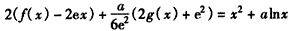 ,
,
即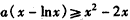 ,①
,①
当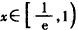 时,lnx<0,∴x-lnx>0,
时,lnx<0,∴x-lnx>0,
当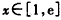 时,lnx≤1≤x,且等号不能同时成立,
时,lnx≤1≤x,且等号不能同时成立,
∴x-lnx>0,
所以,则由①式可得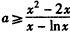 在[
在[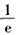 ,e]上恒成立,
,e]上恒成立,
设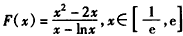 ,
,
又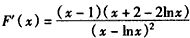 ,
,
令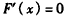 ,得x=1,
,得x=1,
又lnx≤1,
∴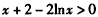 ,
,
所以,当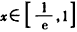 时,
时,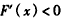 ;
;
当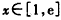 时,
时,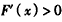 ,
,
所以,函数F(x)在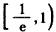 上为减函数,在
上为减函数,在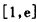 上为增函数,
上为增函数,
又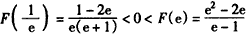 ,
,
故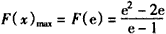 ,
,
所以,实数a的取值范围是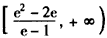 。
。
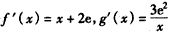 ,
,设函数
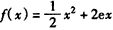 与
与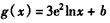 的图象有公共点为
的图象有公共点为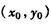 ,
,由题意,得
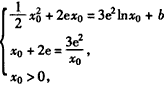 ,
,解得:
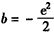 。
。(Ⅱ)由(Ⅰ)知,
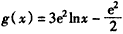 ,
,所以,
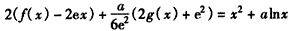 ,
,即
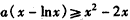 ,①
,①当
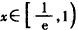 时,lnx<0,∴x-lnx>0,
时,lnx<0,∴x-lnx>0,当
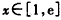 时,lnx≤1≤x,且等号不能同时成立,
时,lnx≤1≤x,且等号不能同时成立,∴x-lnx>0,
所以,则由①式可得
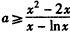 在[
在[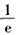 ,e]上恒成立,
,e]上恒成立,设
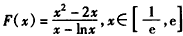 ,
,又
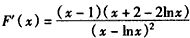 ,
,令
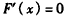 ,得x=1,
,得x=1,又lnx≤1,
∴
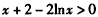 ,
,所以,当
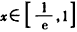 时,
时,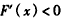 ;
;当
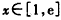 时,
时,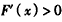 ,
,所以,函数F(x)在
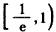 上为减函数,在
上为减函数,在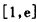 上为增函数,
上为增函数,又
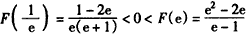 ,
,故
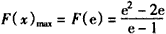 ,
,所以,实数a的取值范围是
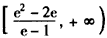 。
。
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目