题目内容
如图所示, 、
、 、
、 是圆
是圆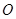 上的三点,
上的三点, 的延长线与线段
的延长线与线段 交于圆内一点
交于圆内一点 ,若
,若
 ,则 ( )
,则 ( )
A. | B. |
C. | D. |

C
解析试题分析:由于 、
、 、
、 三点共线,设
三点共线,设 ,则
,则
 ,由于
,由于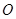 、
、 、
、 三点共线,且点
三点共线,且点 在圆内,点
在圆内,点 在圆上,
在圆上, 与
与 方向相反,则存在
方向相反,则存在 ,使得
,使得 ,因此
,因此 ,
, ,所以
,所以 ,选C.
,选C.
考点:1.共线的平面向量;2.平面向量的线性表示

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设向量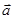 与
与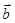 满足
满足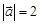 ,
,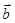 在
在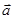 方向上的投影为
方向上的投影为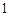 ,若存在实数
,若存在实数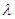 ,使得
,使得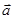 与
与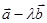 垂直,则
垂直,则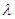 =( )
=( )
A.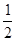 | B.1 | C. 2 | D.3 |
在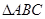 中,D为AB边上一点,
中,D为AB边上一点, ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
[2014·龙岩质检]已知向量a=(1,-1),b=(1,2),向量c满足(c+b)⊥a,(c-a)∥b,则c=( )
| A.(2,1) | B.(1,0) | C.( , , ) ) | D.(0,-1) |
已知向量 =(sinα,cosα),
=(sinα,cosα), =(3,4),且
=(3,4),且 ∥
∥ ,则tanα等于( )
,则tanα等于( )
A. | B.﹣ | C. | D.﹣ |
已知向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c,则λ等于( )
A.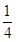 | B.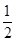 | C.1 | D.2 |

 中,
中, 边的中点,过点
边的中点,过点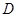 的直线分别交直线
的直线分别交直线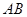 、
、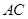 于点
于点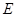 、
、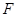 ,若
,若 ,
,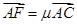 ,其中
,其中 ,则
,则 的最小值是( )
的最小值是( )

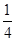

 ,并且
,并且
 的递增区间。
的递增区间。