题目内容
已知双曲线 的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.
的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.(1)求双曲线的方程;
(2)证明:B、P、N三点共线;
(3)求△BMN面积的最小值.
【答案】分析:(I)由题意得A(a,0),B( ,又
,又 ⇒
⇒ …①.
…①. ,由题设知
,由题设知 ⇒
⇒
联立①、②,得a=2,c=4.由此可得双曲线的方程.
(II)由题设得点B(1,0),F(4,0),设直线l的方程为x=ty+4,由 ⇒(3t2-1)y2+24ty+36=0,由此入手可证出B、P、N三点共线.
⇒(3t2-1)y2+24ty+36=0,由此入手可证出B、P、N三点共线.
(III)由题意知x1x2=(ty2+4)(ty2+4)=t2y1y2+4t(y1+y2)+16= ,所以
,所以

 =
= ,由此能求出△BMN面积的最小值.
,由此能求出△BMN面积的最小值.
解答:解:(I)由题意得A(a,0),B( ,又
,又 ⇒
⇒ …①
…①
由 ⇒
⇒ ⇒
⇒
联立①、②,得a=2,c=4
∴双曲线的方程为 .
.
(II)由(I),得点B(1,0),F(4,0),设直线l的方程为x=ty+4
由 ⇒(3t2-1)y2+24ty+36=0
⇒(3t2-1)y2+24ty+36=0
∴
∵(x1-1)y2-(x2-1)(-y1)=x1y2+x2y1-(y1+y2)=(ty1+4)y2+(ty2+4)y1=(ty1+4)y2+(ty2+4)y2


∴向量 与
与 共线,∴B、P、N三点共线.
共线,∴B、P、N三点共线.
(III)∵直线l与双曲线右支相交于M、N两点
∴x1x2=(ty2+4)(ty2+4)=t2y1y2+4t(y1+y2)+16
= ⇒
⇒ ⇒
⇒
∴

=
令u=1-3t2,u∈(0,1]
∴ =
=
由u∈(0,1]⇒
∴ ,即t=0时,△BMN面积最小值为18.
,即t=0时,△BMN面积最小值为18.
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细求解.
 ,又
,又 ⇒
⇒ …①.
…①. ,由题设知
,由题设知 ⇒
⇒
联立①、②,得a=2,c=4.由此可得双曲线的方程.
(II)由题设得点B(1,0),F(4,0),设直线l的方程为x=ty+4,由
 ⇒(3t2-1)y2+24ty+36=0,由此入手可证出B、P、N三点共线.
⇒(3t2-1)y2+24ty+36=0,由此入手可证出B、P、N三点共线.(III)由题意知x1x2=(ty2+4)(ty2+4)=t2y1y2+4t(y1+y2)+16=
 ,所以
,所以

 =
= ,由此能求出△BMN面积的最小值.
,由此能求出△BMN面积的最小值.解答:解:(I)由题意得A(a,0),B(
 ,又
,又 ⇒
⇒ …①
…①由
 ⇒
⇒ ⇒
⇒
联立①、②,得a=2,c=4
∴双曲线的方程为
 .
.(II)由(I),得点B(1,0),F(4,0),设直线l的方程为x=ty+4
由
 ⇒(3t2-1)y2+24ty+36=0
⇒(3t2-1)y2+24ty+36=0∴

∵(x1-1)y2-(x2-1)(-y1)=x1y2+x2y1-(y1+y2)=(ty1+4)y2+(ty2+4)y1=(ty1+4)y2+(ty2+4)y2


∴向量
 与
与 共线,∴B、P、N三点共线.
共线,∴B、P、N三点共线.(III)∵直线l与双曲线右支相交于M、N两点
∴x1x2=(ty2+4)(ty2+4)=t2y1y2+4t(y1+y2)+16
=
 ⇒
⇒ ⇒
⇒
∴


=

令u=1-3t2,u∈(0,1]
∴
 =
=
由u∈(0,1]⇒

∴
 ,即t=0时,△BMN面积最小值为18.
,即t=0时,△BMN面积最小值为18.点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细求解.

练习册系列答案
相关题目
 的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.
的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.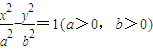 的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.
的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点. 的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.
的右定点为A,右焦点为F,右准线与x轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又OA=2OB,OA•OC=2,过点F的直线与双曲线右交于点M、N,点P为点M关于x轴的对称点.