题目内容
已知函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.
(1)已知函数 ,
, ,判断
,判断 是否具有性质
是否具有性质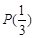 ,并说明理由;
,并说明理由;
(2)已知函数 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(3)若函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,
求证:对任意 且
且 ,函数
,函数 具有性质
具有性质 .
.
 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.(1)已知函数
 ,
, ,判断
,判断 是否具有性质
是否具有性质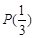 ,并说明理由;
,并说明理由;(2)已知函数
 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;(3)若函数
 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,求证:对任意
 且
且 ,函数
,函数 具有性质
具有性质 .
.(1)具有该性质,证明见解析;(2) ;(3)证明见解析.
;(3)证明见解析.
 ;(3)证明见解析.
;(3)证明见解析.

试题分析:(1)创新定义问题,首先要读懂具有性质P(m)的意思, 对于给定的
 (
( 且
且 ),存在
),存在 ,使得
,使得 ,按照此定义进行判断,假设具有该性质, 设
,按照此定义进行判断,假设具有该性质, 设 ,令
,令 ,解得
,解得
 ,满足定义,故具有性质P(3);(2)m在0到1之间,取一半,看是
,满足定义,故具有性质P(3);(2)m在0到1之间,取一半,看是具有性质P(
 ),如果有,再判断是否有大于
),如果有,再判断是否有大于 的m,没有的话,最大值就是
的m,没有的话,最大值就是 ;(3)构造函数
;(3)构造函数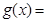
 ,则
,则 ,
, …
… …
… =
=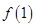 -
-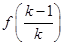 ,相加,有
,相加,有 ,分里面有零和没零进行讨论,得到结论.
,分里面有零和没零进行讨论,得到结论.试题解析:(1)设
 ,即
,即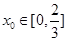
令
 , 则
, 则
解得

 ,
, 所以函数
 具有性质
具有性质
(2)m的最大值为
 .
. 首先当
 时,取
时,取 ,
, 则
 ,
, ,
, 所以函数
 具有性质
具有性质 ,
,假设存在
 ,使得函数
,使得函数 具有性质
具有性质 ,
, 则
 ,
, 当
 时,
时, ,
, ,
, ,
, 当
 时,
时, ,
, ,
, ,
, 所以不存在
 ,使得
,使得 ,
, 故
 的最大值为
的最大值为 .
. (3)任取
 ,
,设
 ,其中
,其中 ,
, 则有
 ,
, ,
, ,
,……
 ,
,……
 ,
,以上各式相加得:
 ,
,当
 中有一个为
中有一个为 时,不妨设为
时,不妨设为 ,
,即
 ,
,则函数
 具有性质
具有性质 ,
,当
 均不为
均不为 时,由于其和为
时,由于其和为 ,则必然存在正数和负数,
,则必然存在正数和负数,不妨设
 其中
其中 ,
, ,
,由于
 是连续的,所以当
是连续的,所以当 时,至少存在一个
时,至少存在一个 ,
, (当
 时,至少存在一个
时,至少存在一个 ),
),使得
 ,
,即
 ,
,故函数
 具有性质
具有性质 .
.
练习册系列答案
相关题目
 定义在区间
定义在区间 都有
都有 且
且 的值;
的值; 且
且 求证:
求证: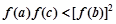 ;
;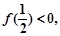 求证:
求证: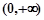 上是增函数.
上是增函数. (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1. 的单调区间,
的单调区间, 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围. 。
。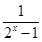 是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为________.
是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为________. 与曲线
与曲线 恰有一个公共点,则实数
恰有一个公共点,则实数 的取值范围为 .
的取值范围为 .


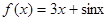 ,则满足不等式
,则满足不等式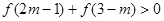 的m的取值范围为 .
的m的取值范围为 .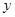 与时间
与时间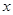 的关系,可选用( )
的关系,可选用( )