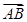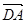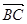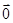题目内容
(本题满分9分)
在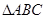 中,
中,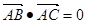 ,
,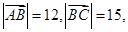
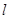 为线段BC的垂直平分线,
为线段BC的垂直平分线,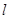 与BC交与点D,E为
与BC交与点D,E为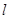 上异于D的任意一点,
上异于D的任意一点,
⑴求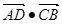 的值。
的值。
⑵判断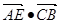 的值是否为一个常数,并说明理由。
的值是否为一个常数,并说明理由。
在
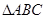 中,
中,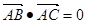 ,
,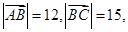
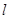 为线段BC的垂直平分线,
为线段BC的垂直平分线,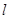 与BC交与点D,E为
与BC交与点D,E为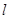 上异于D的任意一点,
上异于D的任意一点,⑴求
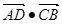 的值。
的值。⑵判断
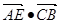 的值是否为一个常数,并说明理由。
的值是否为一个常数,并说明理由。(1)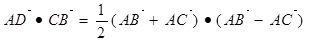 =
=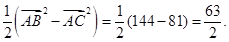
(2)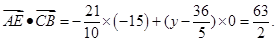 为常数。
为常数。
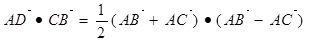 =
=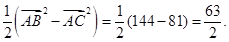
(2)
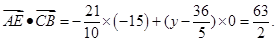 为常数。
为常数。本试题主要是结合了平面向量的基本定理表示未知向量,然后结合已知的长度和角度得到证明。并能利用平面直角坐标系表示数量积来得到。或者运用向量的基本定理表示得到证明。
(1)第一问利用平面向量基本定理表示出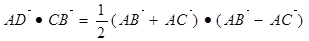 利用已知中的长度和角度得到结论。
利用已知中的长度和角度得到结论。
(2)利用设出平面坐标系来表示点,然后借助于向量的数量积得到结论。
解法1:(1)因为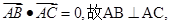 又
又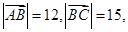 可知
可知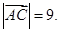
由已知可得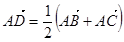 ,
,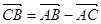 ,
,
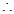
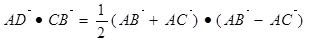
=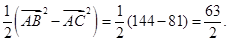 …………4分
…………4分
(2 )
)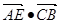 的值为一个常数
的值为一个常数
 L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
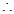
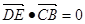
故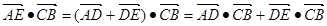 =
=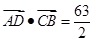 ……9分
……9分
解法2:(1)以D点为原点,BC所在直线为X轴,L所在直线为Y轴建立直角坐标系,可求A(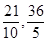 ),此时
),此时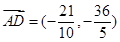 ,
,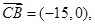
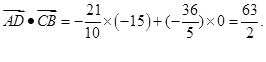 ……4分
……4分
(2)设E点坐标为(0,y)(y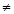 0),此时
0),此时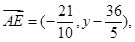
此时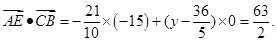 为常数。……9分
为常数。……9分
(1)第一问利用平面向量基本定理表示出
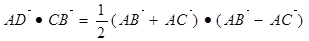 利用已知中的长度和角度得到结论。
利用已知中的长度和角度得到结论。(2)利用设出平面坐标系来表示点,然后借助于向量的数量积得到结论。
解法1:(1)因为
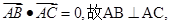 又
又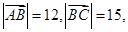 可知
可知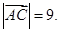
由已知可得
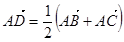 ,
,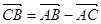 ,
,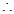
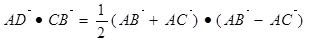
=
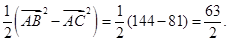 …………4分
…………4分(2
 )
)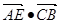 的值为一个常数
的值为一个常数 L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
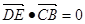
故
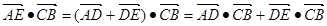 =
=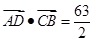 ……9分
……9分解法2:(1)以D点为原点,BC所在直线为X轴,L所在直线为Y轴建立直角坐标系,可求A(
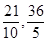 ),此时
),此时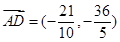 ,
,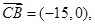
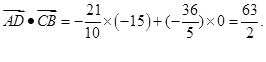 ……4分
……4分(2)设E点坐标为(0,y)(y
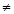 0),此时
0),此时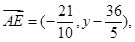
此时
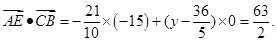 为常数。……9分
为常数。……9分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 中,
中, ,
,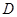 为斜边
为斜边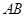 上靠近顶点
上靠近顶点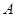 的三等分点.
的三等分点.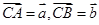 ,求
,求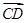 ;
;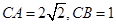 ,求
,求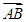 方向上的投影.
方向上的投影.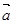 ,
,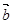 且
且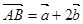 ,
,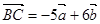 ,
,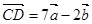 ,则一定共线的三点是
,则一定共线的三点是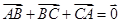
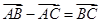
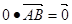
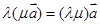
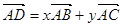 ,则x+y=__________
,则x+y=__________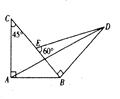
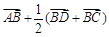 等于( )
等于( )
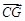
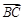
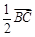
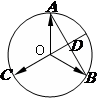
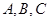 是圆
是圆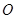 上的三点,
上的三点,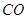 的延长线与线段
的延长线与线段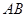 交于圆内一点
交于圆内一点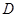 ,若
,若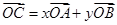 ,则
,则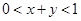
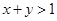
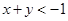
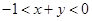
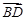 =
=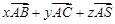 ,则x+y+z=
,则x+y+z= 
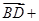
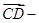
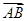 得 ( )
得 ( )