题目内容
已知函数 ,
, 
(Ⅰ)若函数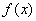 在
在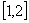 上是减函数,求实数
上是减函数,求实数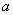 的取值范围;
的取值范围;
(Ⅱ)令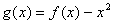 ,是否存在实数
,是否存在实数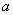 ,当
,当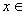
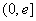 (
(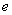 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出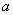 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(III)当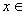
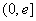 时,证明:
时,证明: 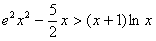
解:(Ⅰ) 在
在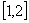 上恒成立,
上恒成立,
令  ,有
,有 得
得 得
得 .
.

③当 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),
综上,存在实数 ,使得当
,使得当 时
时 有最小值3.
有最小值3.
(III)令 ,由(2)知,
,由(2)知, .令
.令 ,
, ,
,
当 时,
时, ,
, 在
在 上单调递增
上单调递增
∴

即


练习册系列答案
相关题目
 B.
B. C.
C. D.
D.

 中,
中,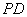 垂直于底面
垂直于底面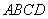 ,底面
,底面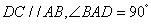 ,且
,且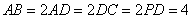 (单位:
(单位: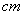 ),
),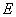 为
为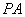 的中点。
的中点。
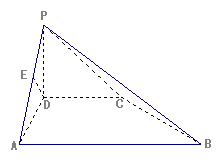 (1)如图,若正视方向与
(1)如图,若正视方向与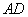 平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积; 平面
平面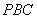 ;
;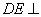 平面
平面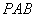 ;
; .若存在
.若存在 的极值点
的极值点 满足
满足 ,则m的取值范围是( )
,则m的取值范围是( ) B.
B.
 D.
D.

 :
: ,使得
,使得 ,则命题
,则命题 是( )
是( ) ,使得
,使得 B.
B.  ,都有
,都有 D.
D.  的焦点坐标为(0,
的焦点坐标为(0, 1),则
1),则 = __ ;
= __ ; ,
, 的最大值是( )
的最大值是( ) .
.
 B.-1
B.-1  .0
.0  .1
.1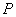 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点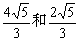 ,过
,过