Question

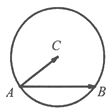
【题目】如图，定圆C半径为2，A为圆C上的一个定点，B为圆C上的动点，若点A，B，C不共线，且| | |对任意t∈（0，+∞）恒成立，则 = ．

Answer 1

【答案】4
【解析】解：| |≥| |=| ﹣ |，

两边平方可得， ﹣2t +t2 ≥ ﹣2 + ，

设 =m，

则22t2﹣2tm﹣（22﹣2m）≥0，

又| | |对任意t∈（0，+∞）恒成立，

则判别式△=4m2+4×4（4﹣2m）≤0，

化简可得（m﹣4）2≤0，

由于（m﹣4）2≥0，则m=4，

即 =4．

故答案为：4．

对| |≥| |=| ﹣ |两边平方，并设 =m，整理可得关于t的一元二次不等式，再由不等式恒成立思想，运用判别式小于等于0，求得m的值．