题目内容
已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称.若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是 ( ).
| A.(3,7) | B.(9,25) | C.(13,49) | D.(9, 49) |
C
解析试题分析: 图像向右平移
图像向右平移 个单位可得
个单位可得 ,函数
,函数 的图象关于点
的图象关于点 对称,那么
对称,那么 图像关于
图像关于 对称,函数为奇函数,且在
对称,函数为奇函数,且在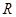 上为增函数,由原不等式可得
上为增函数,由原不等式可得 ,即
,即 ,可化为
,可化为 ,图像知为
,图像知为 圆心,
圆心, 为半径的圆.当
为半径的圆.当 时,
时, 即为右半圆上的点到坐标原点的距离的平方,结合图像可知最大值为
即为右半圆上的点到坐标原点的距离的平方,结合图像可知最大值为 ,最小值为
,最小值为 .
.
考点:函数的奇偶性,数形结合的数学思想方法.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列函数中,既是偶函数又在区间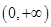 上存在零点的是( )
上存在零点的是( )
A.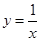 | B.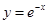 | C.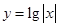 | D.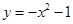 |
设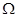 为平面直角坐标系
为平面直角坐标系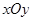 中的点集,从
中的点集,从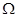 中的任意一点
中的任意一点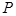 作
作 轴、
轴、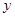 轴的垂线,垂足分别为
轴的垂线,垂足分别为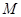 ,
, ,记点
,记点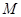 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为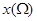 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为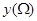 . 若
. 若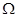 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论:
①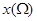 的最大值为
的最大值为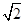 ;
;
②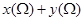 的取值范围是
的取值范围是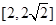 ;
;
③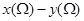 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )
| A.① | B.②③ | C.①② | D.①②③ |
函数 的零点个数是
的零点个数是
| A.1 | B.2 | C.3 | D.4 |
偶函数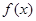 满足
满足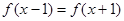 ,且在
,且在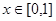 时,
时,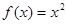 ,则关于
,则关于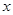 的方程
的方程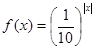 在
在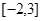 上的根的个数是
上的根的个数是
| A.3 | B.4 | C.5 | D.6 |
(2013•重庆)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x﹣a)的两个零点分别位于区间( )
| A.(a,b)和(b,c)内 | B.(﹣∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 | D.(﹣∞,a)和(c,+∞)内 |
已知函数y=ax2+bx+c(a≠0)的图象经过(-1,3)和(1,1)两点,若0<c<1,则a的取值范围是 ( )
| A.(1,3) | B.(1,2) |
| C.[2,3) | D.[1,3] |
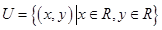 ,
,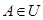 ,
, ,映射
,映射 .对于直线
.对于直线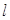 上任意一点
上任意一点 ,
,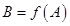 ,若
,若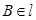 ,我们就称
,我们就称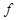 为直线
为直线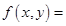
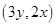 ,则映射
,则映射

 =2,则
=2,则 的值是( )
的值是( )