题目内容
己知椭圆C: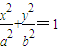 (a>b>0)的离心率为
(a>b>0)的离心率为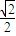 ,不等式
,不等式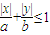 所表示的平面区域的面积为
所表示的平面区域的面积为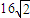 .
.(1)求椭圆C的方程;
(2)设椭圆C的左项点为A,上顶点为B,圆M过A、B两点.当圆心M与原点O的距离最小时,求圆M的方程.
【答案】分析:(1)利用椭圆C的离心率为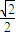 ,可得a=
,可得a=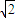 b,根据不等式
b,根据不等式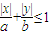 所表示的平面区域的面积为
所表示的平面区域的面积为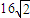 ,可得
,可得 ,由此可求得a,b的值,从而可得椭圆C的方程;
,由此可求得a,b的值,从而可得椭圆C的方程;
(2)确定AB的垂直平分线L的方程,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程,联立可得M的坐标与圆的半径,从而可得圆M的方程.
解答:解:(1)∵椭圆C: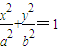 (a>b>0)的离心率为
(a>b>0)的离心率为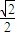 ,∴
,∴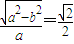
∴a= b①
b①
根据对称性,可得不等式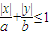 所表示的平面区域是椭圆C的四个顶点为顶点的菱形
所表示的平面区域是椭圆C的四个顶点为顶点的菱形
∵不等式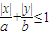 所表示的平面区域的面积为
所表示的平面区域的面积为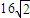 .
.
∴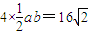 ②
②
由①②解得a=4,b=2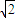
∴椭圆C的方程为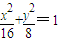 ;
;
(2)由题意,A(-4,0),B(0,2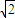 ),可得AB的垂直平分线L的方程为:
),可得AB的垂直平分线L的方程为: =0
=0
点M在L上,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程为: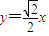
解方程组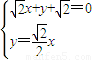 得x=-
得x=- ,y=-
,y=-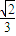
∴M(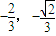 ),此时
),此时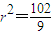
∴圆M的方程为 .
.
点评:本题考查椭圆的标准方程,考查圆的方程,确定圆的圆心与半径是关键.
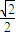 ,可得a=
,可得a=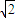 b,根据不等式
b,根据不等式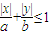 所表示的平面区域的面积为
所表示的平面区域的面积为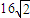 ,可得
,可得 ,由此可求得a,b的值,从而可得椭圆C的方程;
,由此可求得a,b的值,从而可得椭圆C的方程;(2)确定AB的垂直平分线L的方程,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程,联立可得M的坐标与圆的半径,从而可得圆M的方程.
解答:解:(1)∵椭圆C:
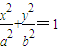 (a>b>0)的离心率为
(a>b>0)的离心率为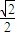 ,∴
,∴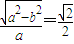
∴a=
 b①
b①根据对称性,可得不等式
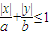 所表示的平面区域是椭圆C的四个顶点为顶点的菱形
所表示的平面区域是椭圆C的四个顶点为顶点的菱形∵不等式
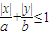 所表示的平面区域的面积为
所表示的平面区域的面积为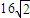 .
.∴
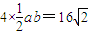 ②
②由①②解得a=4,b=2
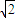
∴椭圆C的方程为
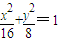 ;
;(2)由题意,A(-4,0),B(0,2
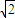 ),可得AB的垂直平分线L的方程为:
),可得AB的垂直平分线L的方程为: =0
=0点M在L上,当圆心M与原点O的距离最小时,OM⊥L,可得OM的方程为:
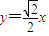
解方程组
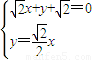 得x=-
得x=- ,y=-
,y=-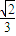
∴M(
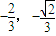 ),此时
),此时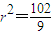
∴圆M的方程为
 .
.点评:本题考查椭圆的标准方程,考查圆的方程,确定圆的圆心与半径是关键.

练习册系列答案
相关题目