题目内容

已知a，b，c∈R⁺，ab=1，a²+b²+c²=9，则a+b+c的最大值为________．

$\text{[math]}$
分析：利用条件，将a+b+c 转化为利用a进行表示，再进行换元，从而可利用柯西不等式求最值．
解答：由题意，∵a，b，c∈R⁺，ab=1，∴ $\text{[math]}$
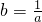
因为a²+b²+c²=9，所以c= $\text{[math]}$
则a+b+c= $\text{[math]}$
设 $\text{[math]}$ ，则 $\text{[math]}$
所以，a+b+c= $\text{[math]}$
根据柯西不等式得 $\text{[math]}$
故答案为 $\text{[math]}$
点评：本题以等式为载体，考查最值，关键是转换为用a进行表示，利用柯西不等式求最值．

练习册系列答案

新语思系列答案

新阅读训练营中考热身赛系列答案

新题型轻松英语听力通系列答案

阳光英语阅读理解与完形填空系列答案

字词句篇与同步作文达标系列答案

新名典阅读方舟系列答案

新理念小学语文阅读训练系列答案

专项突破系列答案

初中文言文全能达标系列答案

新课标初中英语同步听读训练系列答案

相关题目

50、已知a，b，c∈R，证明：a²+4b²+9c²≥2ab+3ac+6bc．

证明：
（1）已知x，y都是正实数，求证：x³+y³≥x²y+xy²，
（2）已知a，b，c∈R⁺，且a+b+c=1，求证：a2+b2+c2 ≥

已知a，b，c∈R₊且满足a+2b+3c=1，则

的最小值为

（1）已知a，b，c∈R，且a+b+c=1，求证：a²+b²+c²≥

；
（2）a，b，c为互不相等的正数，且abc=1，求证：

已知a，b，c∈R，且a＞b，那么下列不等式中成立的是（　　）

C．2^-a＞2^-b