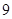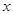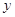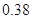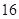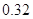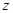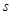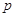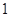题目内容
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛.该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一•二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一•二班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
(Ⅱ)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一•二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一•二班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
分析:(I)根据样本容量,频率和频数之间的关系得到要求的几个数据,注意[80,90)小组数据得出样本容量,从而进一步得出表中的x,y,z,s,p的值.
(II)①设“甲不在第一位、乙不在第六位”为事件A,根据相互独立事件的概率公式得到结果.
②随机变量X的可能取值为0,1,2,结合变量对应的概率,写出分布列和期望.
(II)①设“甲不在第一位、乙不在第六位”为事件A,根据相互独立事件的概率公式得到结果.
②随机变量X的可能取值为0,1,2,结合变量对应的概率,写出分布列和期望.
解答:解:(Ⅰ)由题意知,由[80,90)上的数据,
根据样本容量,频率和频数之间的关系得到n=
=50,
∴x=
=0.18,
y=19,z=6,s=0.12,p=50--------------(3分)
(Ⅱ)由(Ⅰ)知,参加决赛的选手共6人,--------------(4分)
①设“甲不在第一位、乙不在第六位”为事件A,
则P(A)=
=
所以甲不在第一位、乙不在第六位的概率为
.--------------(6分)
②随机变量X的可能取值为0,1,2--------------(7分)
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,--------------(10分)
随机变量X的分布列为:
--------------(11分)
因为 EX=0×
+1×
+2×
=1,
所以随机变量X的数学期望为1.--------------(12分)
根据样本容量,频率和频数之间的关系得到n=
| 16 |
| 0.32 |
∴x=
| 9 |
| 50 |
y=19,z=6,s=0.12,p=50--------------(3分)
(Ⅱ)由(Ⅰ)知,参加决赛的选手共6人,--------------(4分)
①设“甲不在第一位、乙不在第六位”为事件A,
则P(A)=
| ||||||||
|
| 7 |
| 10 |
所以甲不在第一位、乙不在第六位的概率为
| 7 |
| 10 |
②随机变量X的可能取值为0,1,2--------------(7分)
P(X=0)=
| ||||
|
| 1 |
| 5 |
P(X=1)=
| ||||||||
|
| 3 |
| 5 |
P(X=2)=
| ||||
|
| 1 |
| 5 |
随机变量X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
因为 EX=0×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
所以随机变量X的数学期望为1.--------------(12分)
点评:本小题考查频率、频数和样本容量之间的关系,考查离散型随机变量的随机变量的分布列及数学期望,是一个综合题.

练习册系列答案
相关题目
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为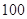 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
|
分数(分数段) |
频数(人数) |
频率 |
|
[60,70) |
|
|
|
[70,80) |
|
|
|
[80,90) |
|
|
|
[90,100) |
|
|
|
合 计 |
|
|
(Ⅰ)求出上表中的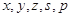 的值;
的值;
(Ⅱ)按规定,预赛成绩不低于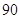 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一·二班在决赛中进入前三名的人数为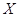 ,求
,求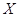 的分布列和数学期望.
的分布列和数学期望.
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛.该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
(Ⅱ)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一•二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一•二班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛.该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一•二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一•二班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
(Ⅱ)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一•二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一•二班在决赛中进入前三名的人数为X,求X的分布列和数学期望.