题目内容
如图5所示,四棱锥P—ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°.PD垂直底面ABCD,PD=2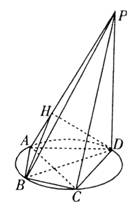
图5
(1)求BD与平面ABP所成角θ的正弦值;
(2)证明△EFG是直角三角形;
(3)当![]() =
=![]() 时,求△EFG的面积.
时,求△EFG的面积.
(1)解:过点D作DH⊥PA,垂足为H,连结BH,

∵PD⊥平面ABC,∴PD⊥AB.
∵BD是直径,
∴AB⊥AD,
∴AB⊥平面PAD.
又HD![]() 平面PAD,
平面PAD,
∴AB⊥HD.
∴HD⊥平面PAB.
因此∠DBH就是BD与平面PAD所成的角.
∵AD=![]() R,AP=
R,AP=![]() ,
,
∴DH=![]() R.
R.
sinθ=sin∠DBH=![]() =
=![]() .
.
(2)证明:∵EG∥BC,

∴![]() .又
.又![]() ,
,
∴![]() .∴GF∥PD.又PD⊥BC,
.∴GF∥PD.又PD⊥BC,
∴EG⊥GF.∴△EFG是直角三角形.
(3)解:∵![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
又BC=![]() R,∴EG=
R,∴EG=![]() .
.
同理,GF=![]() PD=
PD=![]() ×2
×2![]() R=
R=![]() R,
R,
∴S△EFG=![]() ×
×![]() R×
R×![]() R=
R=![]() R2.
R2.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=
如图所示,四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=
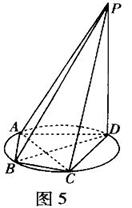

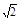 a,则它的5个面中,互相垂直的面有
对.
a,则它的5个面中,互相垂直的面有
对.