题目内容

（2013•闸北区一模）设函数f(x)=
x•2x，x≥0
x-2，x＜0.
则方程f（x）=x2+1有实数解的个数为
2
2
．
分析：方程f（x）=x2+1的实数解的个数问题转化为图象的交点问题，作图分析即得答案．
解答：解：画出f(x)=
x•2x，x≥0
x-2，x＜0.
与y=x2+1的图象，有两个交点，

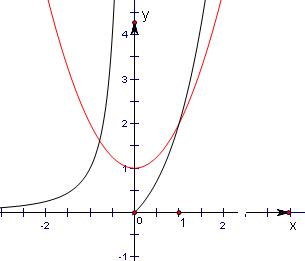
故方程f（x）=x2+1的实数解的个数为2个．
故答案为：2．
点评：华罗庚曾说过：“数缺形时少直观，形缺数时难入微．数形结合百般好，隔离分家万事非．”数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．
练习册系列答案
相关题目
（2013•闸北区一模）已知（1+px2）5的展开式中，x6的系数为80，则p=
2
2
．
（2013•闸北区一模）设{an}是公比为
1
2
的等比数列，且
lim
n→∞
(a1+a3+a5+…+a2n-1)=4，则a1=
3
3
．
（2013•闸北区一模）函数f(x)=
21-x，x＜0
f(x-1)，x＞0.
，则f（3.5）的值为
2
2
2
2
．
（2013•闸北区一模）一人在海面某处测得某山顶C的仰角为α（0°＜α＜45°），在海面上向山顶的方向行进m米后，测得山顶C的仰角为90°-α，则该山的高度为
1
2
mtan2α
1
2
mtan2α
米．（结果化简）
（2013•闸北区一模）设点F1（-c，0），F2（c，0）分别是椭圆C：
x2
a2
+y2=1(a＞1)的左、右焦点，P为椭圆C上任意一点，且
PF1
•
PF2
最小值为0．
（1）求椭圆C的方程；
（2）设定点D（m，0），已知过点F2且与坐标轴不垂直的直线l与椭圆交于A、B两点，满足|AD|=|BD|，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网