题目内容
已知椭圆
分析:计算三角形的面积有多种公式可供选择,其中与已知条件联系最密切的当为S△=![]() |PF1|·|PF2|·sinθ,所以应围绕|PF1|·|PF2|进行计算.
|PF1|·|PF2|·sinθ,所以应围绕|PF1|·|PF2|进行计算.
解:如图,由椭圆第一定义,有|PF1|+|PF2|=2a,而在△F1PF2中,由余弦定理有?
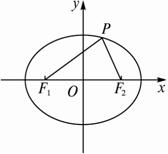
|PF1|2+|PF2|2-2|PF1|·|PF2|cosθ=|F1F2|2=4c2,?
∴(|PF1|+|PF2|)2-2|PF1|·|PF2|-2|PF1|·|PF2|cosθ=4c2,?
即4(a2-c2)=2|PF1|·|PF2|(1+cosθ).?
∴S△PF1F2=![]() |PF1|·|PF2|sinθ?
|PF1|·|PF2|sinθ?
=b2![]() =b2tan
=b2tan![]() .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆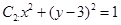 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切.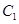 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C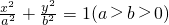 上任一点P到两个焦点的距离的和为
上任一点P到两个焦点的距离的和为 ,P与椭圆长轴两顶点连线的斜率之积为
,P与椭圆长轴两顶点连线的斜率之积为 .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).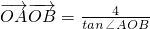 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;