题目内容
已知球的直径AB=2,C、D是该球球面上的两点,且BC=CD=DB=
,则三棱锥A-BCD的体积为
.
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
分析:取CD中点E,连接AE、BE,可证出△ACD、△BCD都是等边三角形,并且CD⊥平面ABE,由此将三棱锥A-BCD的体积分为三棱锥C-ABE与三棱锥D-ABE的体积之和,结合题中数据算出△ABE中的面积,用锥体体积公式即可求出三棱锥A-BCD的体积.
解答:解:∵AB是球的直径,D、C两点在球面上
∴∠ACB=∠ADB=90°
∵AB=2,BC=BD=
∴AC=AD=
=CD
取CD中点E,连接AE、BE
∵等边△ACD中,AE⊥CD,等边△BCD中,BE⊥CD,BE∩AE=E
∴CD⊥平面ABE
∵△ABE中,BE=AE=
×
=
,AB=2
∴△ABE中的面积S=
由此可得三棱锥A-BCD的体积V=VC-ABE+VD-ABE=
S△ABE•CE+
S△ABE•DE=
S△ABE•CD=
×
×
=
故答案为:

∴∠ACB=∠ADB=90°
∵AB=2,BC=BD=
| 2 |
∴AC=AD=
| 2 |
取CD中点E,连接AE、BE
∵等边△ACD中,AE⊥CD,等边△BCD中,BE⊥CD,BE∩AE=E
∴CD⊥平面ABE
∵△ABE中,BE=AE=
| ||
| 2 |
| 2 |
| ||
| 2 |
∴△ABE中的面积S=
| ||
| 2 |
由此可得三棱锥A-BCD的体积V=VC-ABE+VD-ABE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题给出特殊的球内接三棱锥,求它的体积,着重考查了球内接多面体、线面垂直的判定定理和锥体体积公式等知识,属于基础题.

练习册系列答案
相关题目
 ,则三棱锥A-BCD的体积为________.
,则三棱锥A-BCD的体积为________.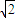 ,则三棱锥A-BCD的体积为 .
,则三棱锥A-BCD的体积为 .