题目内容
 已知三棱柱ABC-A1B1C1,侧面AA1C1C⊥侧面ABB1A1,AA1=A1C=CA=2,
已知三棱柱ABC-A1B1C1,侧面AA1C1C⊥侧面ABB1A1,AA1=A1C=CA=2,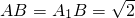 .
.
(1)求证:AA1⊥BC;
(2)求二面角A-BC-A1的余弦值;
(3)若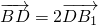 ,在线段CA1上是否存在一点E,使得DE∥平
,在线段CA1上是否存在一点E,使得DE∥平
面ABC?若存在,求出CE的长;若不存在,请说明理由.
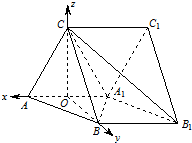 证明:(1)取AA1中点O,连接CO,BO.
证明:(1)取AA1中点O,连接CO,BO.∵CA=CA1,
∴CO⊥AA1,
又∵BA=BA1,
∴BO⊥AA1,
∵BO∩CO=O,
∴AA1⊥平面BOC,
∵BC?平面BOC,
∴AA1⊥BC.
解:(2)由(1)CO⊥AA1,又侧面AA1C1C⊥侧面ABB1A1,侧面AA1C1C∩侧面ABB1A1=AA1
∴CO⊥平面ABB1A1,而BO⊥AA1,
∴OA,OB,OC两两垂直.
如图,以O为坐标原点,分别以OA,OB,OC为x,y,z轴建立空间直角坐标系O-xyz.则有
 由对称性知,二面角A-BC-A1的大小为二面角A-BC-O的两倍
由对称性知,二面角A-BC-A1的大小为二面角A-BC-O的两倍设
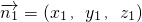 是平面ABC的一个法向量,
是平面ABC的一个法向量,∵
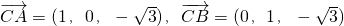 ,
,由
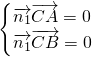 即
即 解得
解得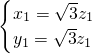
令z1=1,∴
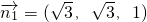 .
.又
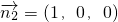 是平面OBC的一个法向量,
是平面OBC的一个法向量,设二面角A-BC-O为θ,则
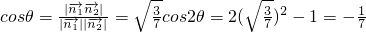 ,
,所以二面角A-BC-A1的余弦值是
 .
.(3)假设存在满足条件的点E,∵
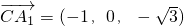 ,故可设
,故可设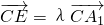 =
=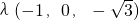 ,
,则
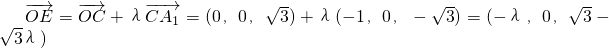 ,
,∵
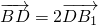 ,
,∴
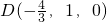 ,
,∴
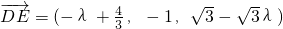 ,
,∵DE∥平面ABC,
∴
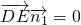 ,
,即
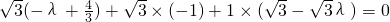 ,解得
,解得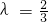 ,
,∴
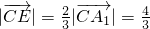
分析:(1)取AA1中点O,连接CO,BO,由已知中A1C=CA=2,
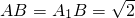 .易得CO⊥AA1且BO⊥AA1,结合线面垂直的判定定理可得AA1⊥平面BOC,进而由线面垂直的性质定理得到AA1⊥BC;
.易得CO⊥AA1且BO⊥AA1,结合线面垂直的判定定理可得AA1⊥平面BOC,进而由线面垂直的性质定理得到AA1⊥BC;(2)结合(1)的结论可得OA,OB,OC两两垂直,以O为坐标原点,分别以OA,OB,OC为x,y,z轴建立空间直角坐标系O-xyz.我们求出平面ABC的一个法向量和平面OBC的一个法向量,代入向量夹角公式,即可得到二面角A-BC-A1的余弦值;
(3)设
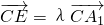 ,结合DE∥平面ABC,
,结合DE∥平面ABC,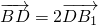 ,我们可以构造一个关于λ的方程,解方程求出λ的值,即可得到向量
,我们可以构造一个关于λ的方程,解方程求出λ的值,即可得到向量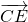 模的大小.
模的大小.点评:本题考查的知识点是用空间向量求平面间的夹角,空间中直线与直线之间的位置关系,向量语言表述线面的垂直、平行关系,其中(1)的关键是证得CO⊥AA1且BO⊥AA1,(2)的关键是求出平面ABC的一个法向量和平面OBC的一个法向量,(3)的关键是根据已知条件求出λ的值.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|