题目内容
1.过点A(-2,3)作直线与抛物线y2=8x在第一象限相切于点B,记抛物线的焦点为F,则直线BF的斜率为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 求出第一象限的抛物线方程,设出切点,并求导,得到切线AB的斜率,再由两点的斜率公式得到方程,解出方程求出切点,再由两点的斜率公式求出BF的斜率.
解答 解:抛物线C:y2=8x,在第一象限的方程为y=2$\sqrt{2}x$,
设切点B(m,n),则n=2$\sqrt{2}$m,
又导数y′=2$\sqrt{2}$•$\frac{1}{2}$•$\frac{1}{\sqrt{x}}$,则在切点处的斜率为$\frac{\sqrt{2}}{\sqrt{m}}$,
∴$\frac{n-3}{m+2}$=$\frac{\sqrt{2}}{\sqrt{m}}$即$\sqrt{2}$m+2$\sqrt{2}$=2$\sqrt{2}$m-3$\sqrt{m}$,
解得$\sqrt{m}$=2$\sqrt{2}$(-$\frac{\sqrt{2}}{2}$舍去),
∴切点B(8,8),又F(2,0),
∴直线BF的斜率为$\frac{8-0}{8-2}$=$\frac{4}{3}$,
故选:D.
点评 本题主要考查抛物线的方程和性质,同时考查直线与抛物线相切,运用导数求切线的斜率等,是一道中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2x,若对于任意的x∈[a,a+2],均有f(x+a)≥f2(x),则实数a取值范围是( )
| A. | [1,+∞) | B. | $[-\frac{1}{2},1)$ | C. | $(-∞,-\frac{3}{2}]$ | D. | (0,+∞) |
16.若6<a<10,$\frac{a}{2}$≤b≤2a,c=a+b,那么c的取值范围是( )
| A. | 9≤c≤18 | B. | 15<c<30 | C. | 9≤c≤30 | D. | 9<c<30 |
10.命题“若对任意?n∈N*都有an<an+1,则数列{an}是递增数列”的逆否命题是( )
| A. | 若数列{an}是递减数列,则对任意n∈N*都有an≥an+1 | |
| B. | 若数列{an}是递减数列,则存在n∈N*都有an≥an+1 | |
| C. | 若数列{an}不是递增数列,则对任意n∈N*都有an≥an+1 | |
| D. | 若数列{an}不是递增数列,则存在n∈N*都有an≥an+1 |
11.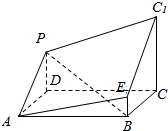 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则点F到平面AEC的距离为( )
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则点F到平面AEC的距离为( )
 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则点F到平面AEC的距离为( )
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则点F到平面AEC的距离为( )| A. | $\frac{1}{7}$ | B. | $\frac{\sqrt{21}}{7}$ | C. | $\frac{4\sqrt{21}}{7}$ | D. | $\frac{8}{7}$ |