题目内容
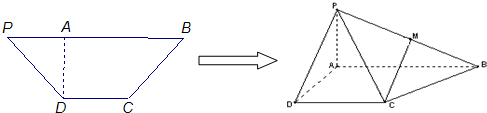
如图,在等腰梯形PDCB中,PB=3,DC=1,PD=BC= ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)若M是侧棱PB中点,截面AMC把几何体分成的两部分,求这两部分的体积之比.
证明:(Ⅰ)依题意知PA=1,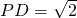 ∴AD⊥AB,
∴AD⊥AB,
又CD∥AB∴CD⊥AD(3分)
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
由面面垂直的性质定理知,CD⊥平面PAD(6分)
(Ⅱ)解:设N是AB的中点,连接MN,依题意,PA⊥AD,PA⊥AB,
所以,PA⊥面ABCD,因为MN∥PA,
所以MN⊥面ABCD.(8分) (10分)
(10分) (11分)
(11分)
所以, (12分)
(12分)
VPADCM:VMACB=两部分体积比为2:1(14分)
分析:(Ⅰ)依题意通过计算,以及平面PAD⊥平面ABCD,由面面垂直的性质定理,证明CD⊥平面PAD.
(Ⅱ)设N是AB的中点,连接MN,依题意,证明PA⊥面ABCD,MN⊥面ABCD,计算 与
与 ,得到VPADCM=VPADCB-VMACB,求出VPADCM:VMACB=两部分体积比.
,得到VPADCM=VPADCB-VMACB,求出VPADCM:VMACB=两部分体积比.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.
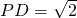 ∴AD⊥AB,
∴AD⊥AB,又CD∥AB∴CD⊥AD(3分)
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
由面面垂直的性质定理知,CD⊥平面PAD(6分)
(Ⅱ)解:设N是AB的中点,连接MN,依题意,PA⊥AD,PA⊥AB,
所以,PA⊥面ABCD,因为MN∥PA,
所以MN⊥面ABCD.(8分)
 (10分)
(10分) (11分)
(11分)所以,
 (12分)
(12分)VPADCM:VMACB=两部分体积比为2:1(14分)
分析:(Ⅰ)依题意通过计算,以及平面PAD⊥平面ABCD,由面面垂直的性质定理,证明CD⊥平面PAD.
(Ⅱ)设N是AB的中点,连接MN,依题意,证明PA⊥面ABCD,MN⊥面ABCD,计算
 与
与 ,得到VPADCM=VPADCB-VMACB,求出VPADCM:VMACB=两部分体积比.
,得到VPADCM=VPADCB-VMACB,求出VPADCM:VMACB=两部分体积比.点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
相关题目
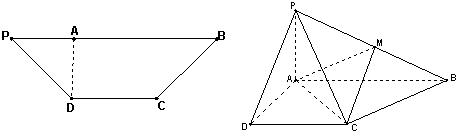
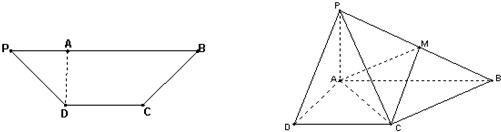
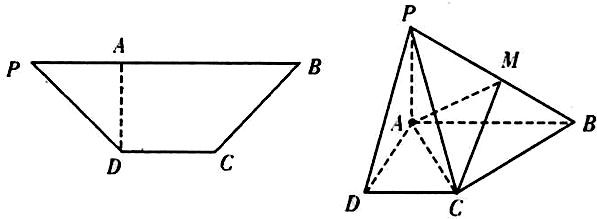
 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=