Question

已知数列{a_n}中，a₁=，（n≥2，n∈N*），数列{b_n}满足，（n∈N*）． （1）求证：数列{b_n}是等差数列；
（2）求数列{a_n}中的最大项和最小项，并说明理由。

Answer 1

（1）证明：因为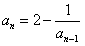（n≥2，n∈N*），，
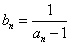所以，当n≥2时，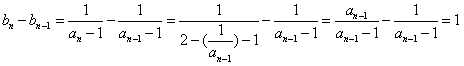
，
，
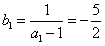∴数列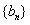是以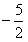为首项，1为公差的等差数列。
（2）解：由（1）知，，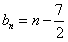
则，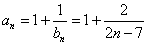
设函数，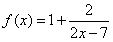
f（x）在区间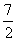（-∞，）和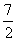（，+∞）内为减函数，
又f（3）=-1，f（4）=3，
所以，当n=3时，a_n取得最小值-1；当n=4时，a_n取得最大值3。