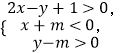Question

【题目】曲线y=1+ 与直线y=k（x﹣2）+4有两个交点，则实数k的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：根据题意画出图形，如图所示：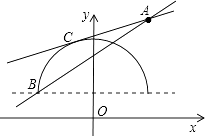
由题意可得：直线l过A（2，4），B（﹣2，1），
又曲线 图象为以（0，1）为圆心，2为半径的半圆，
当直线l与半圆相切，C为切点时，圆心到直线l的距离d=r，即 =2，
解得：k= ；
当直线l过B点时，直线l的斜率为 = ，
则直线l与半圆有两个不同的交点时，实数k的范围为 ．
故答案为：D
要求的实数k的取值范围即为直线l斜率的取值范围，主要求出斜率的取值范围，方法为：曲线 表示以（0，1）为圆心，2为半径的半圆，在坐标系中画出相应的图形，直线l与半圆有不同的交点，故抓住两个关键点：当直线l与半圆相切时，圆心到直线的距离等于圆的半径，利用点到直线的距离公式列出关于k的方程，求出方程的解得到k的值；当直线l过B点时，由A和B的坐标求出此时直线l的斜率，根据两种情况求出的斜率得出k的取值范围．