题目内容
对于定义域为 的函数
的函数 ,若同时满足:①
,若同时满足:① 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间
 ,使
,使 在
在 上的值域为
上的值域为 ;那么把函数
;那么把函数 (
( )叫做闭函数.
)叫做闭函数.
(1) 求闭函数 符合条件②的区间
符合条件②的区间 ;
;
(2) 若 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.
 的函数
的函数 ,若同时满足:①
,若同时满足:① 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间
 ,使
,使 在
在 上的值域为
上的值域为 ;那么把函数
;那么把函数 (
( )叫做闭函数.
)叫做闭函数.(1) 求闭函数
 符合条件②的区间
符合条件②的区间 ;
;(2) 若
 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.(1)区间为[-1,0]或[-1,1]或[0,1 ](2)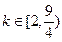
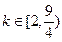
(1)由题意,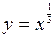 在
在 上递增,则
上递增,则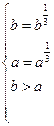 ,……………………2分
,……………………2分
解得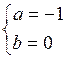 或
或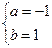 或
或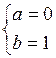 …………………………………………………4分
…………………………………………………4分
所以,所求的区间为[-1,0]或[-1,1]或[0,1 ]. ………………………………5分
(2)若 是闭函数,则存在区间
是闭函数,则存在区间 ,在区间
,在区间 上,
上,
函数 的值域为
的值域为 …………………………………………6分
…………………………………………6分
容易证明函数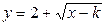 在定义域内单调递增,
在定义域内单调递增,
∴ …………………………………………………………………7分
…………………………………………………………………7分
∴ 为方程
为方程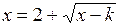 的两个实数根. ………………………………9分
的两个实数根. ………………………………9分
即方程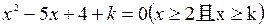 有两个不相等的实根.
有两个不相等的实根.
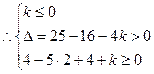 或
或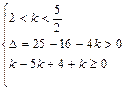 ………………………………………12分
………………………………………12分
解得 ,综上所述,
,综上所述,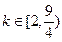 ……………………………………………………14分
……………………………………………………14分
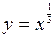 在
在 上递增,则
上递增,则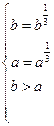 ,……………………2分
,……………………2分 解得
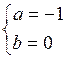 或
或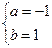 或
或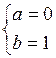 …………………………………………………4分
…………………………………………………4分 所以,所求的区间为[-1,0]或[-1,1]或[0,1 ]. ………………………………5分
(2)若
 是闭函数,则存在区间
是闭函数,则存在区间 ,在区间
,在区间 上,
上,函数
 的值域为
的值域为 …………………………………………6分
…………………………………………6分容易证明函数
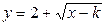 在定义域内单调递增,
在定义域内单调递增,∴
 …………………………………………………………………7分
…………………………………………………………………7分∴
 为方程
为方程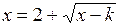 的两个实数根. ………………………………9分
的两个实数根. ………………………………9分即方程
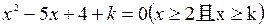 有两个不相等的实根.
有两个不相等的实根. 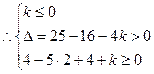 或
或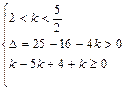 ………………………………………12分
………………………………………12分解得
 ,综上所述,
,综上所述,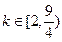 ……………………………………………………14分
……………………………………………………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 五个方面的多元评价指标,并通过经验公式样
五个方面的多元评价指标,并通过经验公式样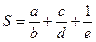 来计算各班的综合得分,S的值越高则评价效果越好,若某班在自测过程中各项指标显示出
来计算各班的综合得分,S的值越高则评价效果越好,若某班在自测过程中各项指标显示出 ,则下阶段要把其中一个指标的值增加1个单位,而使得S的值增加最多,那么该指标应为 .(填入
,则下阶段要把其中一个指标的值增加1个单位,而使得S的值增加最多,那么该指标应为 .(填入 ,
, (其中
(其中 ,且
,且 ).
). 请你推测
请你推测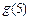 能否用
能否用 来表示;
来表示; 中,猜想
中,猜想 的最大值,并证明之。
的最大值,并证明之。 ; ⑵
; ⑵ ,归纳其特点可以获得一个猜想是:
,归纳其特点可以获得一个猜想是: .
. 理是类比推理的是( )
理是类比推理的是( ) 切偶数能被2整除,2100是偶数,故2100能被2整数
切偶数能被2整除,2100是偶数,故2100能被2整数