题目内容

已知在数列{an}中，a1=，且有an+1=(n∈N*).

(Ⅰ)求数列{an}的通项公式；

(Ⅱ)若bn=，数列{bn}的前n和为Sn,证明：Sn＜1；

(Ⅲ)若，且{cn}的前n项和为Tn，求Tn值.

解：(1)将原式变形为,

即,,

那么数列{}是以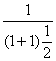+1=2为首项,以2为公比的等比数列,

即：,则an=.

(Ⅱ)由(Ⅰ)知bn=,

这样Sn=＜1. 

(Ⅲ)由(Ⅰ)知cn=,这样Tn=2×+3×+4×+…+(n+1),

则Tn=2×+3×+4×+…+(n+1).

两式作差得：

Tn=1+

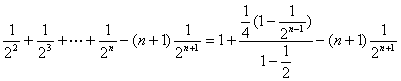
,即：Tn=-(n+1)+3,这样Tn=3.

练习册系列答案
相关题目
已知在数列{an}中，a1=1，当n≥2时，其前n项和Sn满足Sn2=an(Sn-
1
2
)．
（Ⅰ） 求Sn的表达式；
（Ⅱ） 设bn=
Sn
2n+1
，求数列{bn}的前n项和Tn．
已知在数列{an}中，a1=7，an+1=
7anan+7
，计算这个数列的前4项，并猜想这个数列的通项公式．
已知在数列{an}中，an≠0，（n∈N*）．求证：“{an}是常数列”的充要条件是“{an}既是等差数列又是等比数列”．
（2011•河北区一模）已知在数列{an}中，Sn是前n项和，满足Sn+an=n，（n=1，2，3，…）．
（Ⅰ）求a1，a2，a3的值；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）令bn=（2-n）（an-1）（n=1，2，3，…），求数列{bn}的前n项和Tn．
已知在数列{an}中，a1=
1
2
，Sn是其前n项和，且Sn=n2an-n（n-1）．
（1）证明：数列{
n+1
n
Sn}是等差数列；
（2）令bn=（n+1）（1-an），记数列{bn}的前n项和为Tn．
①求证：当n≥2时，Tn2＞2(
T2
2
+
T3
3
+…+
Tn
n
)；
②）求证：当n≥2时，bn+1+bn+2+…+b2n＜
4
5
-
1
2n+1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网