题目内容
已知{an}是等差数列,其前n项和为Sn,已知a3=5,S9=81,
①求数列{an}的通项公式;
②设bn=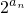 ,证明{bn}是等比数列,并求其前n项和Tn.
,证明{bn}是等比数列,并求其前n项和Tn.
③设cn=an•bn,求数列{cn} 的前n项的和Mn.
解:①∵等差数列,a3=5,S9=81,
∴ ,
,
解得a1=1,d=2,
∴an=1+(n-1)×2=2n-1.
②∵bn=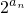 ,
,
∴bn=22n-1= ,
,
 ,
, ,
,
 ,
,
∴{bn}是以2以道貌岸然项,以4为公比的等比数列.
Tn= =
= .
.
③∵cn=an•bn=(2n-1) ,
,
∴Mn=(2-1) +(2×
+(2× •
• +(2×3-1)
+(2×3-1) +…+
+…+ +(2n-1)
+(2n-1) ×4n,
×4n,
 +
+ +…+
+…+ +(2n-1)
+(2n-1) ×4n+1,
×4n+1,
∴ 4n+1
4n+1
=2+ -(2n-1)
-(2n-1)
=2+ ,
,
∴ .
.
分析:①由等差数列中,a3=5,S9=81,利用通项公式和前n项和公式列出方程组 ,求出a1=1,d=2,由此能求出an=2n-1.
,求出a1=1,d=2,由此能求出an=2n-1.
②由bn=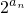 ,知bn=22n-1=
,知bn=22n-1= ,由此能够证明{bn}是以2以道貌岸然项,以4为公比的等比数列.并能求出其前n项和Tn.
,由此能够证明{bn}是以2以道貌岸然项,以4为公比的等比数列.并能求出其前n项和Tn.
③由cn=an•bn=(2n-1) ,知Mn=(2-1)
,知Mn=(2-1) +(2×
+(2× •
• +(2×3-1)
+(2×3-1) +…+
+…+ +(2n-1)
+(2n-1) ×4n,由错位相减法能够求出数列{cn} 的前n项的和Mn.
×4n,由错位相减法能够求出数列{cn} 的前n项的和Mn.
点评:本题考查数列通项公式的求法,等比数列的证明,前n项和的求法,解题时要认真审题,仔细解答,注意错位相减求和法的灵活运用.
∴
 ,
,解得a1=1,d=2,
∴an=1+(n-1)×2=2n-1.
②∵bn=
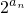 ,
,∴bn=22n-1=
 ,
, ,
, ,
, ,
,∴{bn}是以2以道貌岸然项,以4为公比的等比数列.
Tn=
 =
= .
.③∵cn=an•bn=(2n-1)
 ,
,∴Mn=(2-1)
 +(2×
+(2× •
• +(2×3-1)
+(2×3-1) +…+
+…+ +(2n-1)
+(2n-1) ×4n,
×4n, +
+ +…+
+…+ +(2n-1)
+(2n-1) ×4n+1,
×4n+1,∴
 4n+1
4n+1=2+
 -(2n-1)
-(2n-1)
=2+
 ,
,∴
 .
.分析:①由等差数列中,a3=5,S9=81,利用通项公式和前n项和公式列出方程组
 ,求出a1=1,d=2,由此能求出an=2n-1.
,求出a1=1,d=2,由此能求出an=2n-1.②由bn=
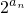 ,知bn=22n-1=
,知bn=22n-1= ,由此能够证明{bn}是以2以道貌岸然项,以4为公比的等比数列.并能求出其前n项和Tn.
,由此能够证明{bn}是以2以道貌岸然项,以4为公比的等比数列.并能求出其前n项和Tn.③由cn=an•bn=(2n-1)
 ,知Mn=(2-1)
,知Mn=(2-1) +(2×
+(2× •
• +(2×3-1)
+(2×3-1) +…+
+…+ +(2n-1)
+(2n-1) ×4n,由错位相减法能够求出数列{cn} 的前n项的和Mn.
×4n,由错位相减法能够求出数列{cn} 的前n项的和Mn.点评:本题考查数列通项公式的求法,等比数列的证明,前n项和的求法,解题时要认真审题,仔细解答,注意错位相减求和法的灵活运用.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 满足:
满足: .
.