题目内容
设甲:函数 的值域为
的值域为 ,乙:函数
,乙:函数 有四个单调区间,那么甲是乙的( )
有四个单调区间,那么甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
B.
解析试题分析:函数 的值域为
的值域为 ,意味着能取到
,意味着能取到 的实数值,所以
的实数值,所以 ;函数
;函数 有四个单调区间,意味着
有四个单调区间,意味着 有两个不同零点,所以
有两个不同零点,所以 ,故甲是乙的必要不充分条件,选B。
,故甲是乙的必要不充分条件,选B。
考点:本题主要考查充要条件的概念,对数函数的值域,二次函数的单调性。
点评:典型题,充要条件的判断问题,已是高考考查的保留题型之一,往往具有一定的综合性。充要条件的判断有:定义法、等价关系法、集合关系法。

练习册系列答案
相关题目
命题“ ,都有
,都有 ”的否定是( )
”的否定是( )
A.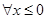 ,都有 ,都有 | B. ,都有 ,都有 |
C. ,使得 ,使得 | D. ,使得 ,使得 |
命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,假命题的个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
下列命题中正确的是( )
A. | B. |
C. | D.单位向量都相等 |
“ ”是“
”是“ ”的
”的
| A.充分而不必要条件 | B.必要而充分不条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题“ ”为假,且“
”为假,且“ ”为假,则( )
”为假,则( )
A. 或 或 为假 为假 | B. 假 假 | C. 真 真 | D.不能判断 的真假 的真假 |
a=0是复数z=a+bi(a,b∈R)为纯虚数的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 、
、 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: ,给出下列三个命题:
,给出下列三个命题: