题目内容
已知左右焦点分别为F1,F2的椭圆 上存在一点P使PF1⊥PF2,直线PF2交椭圆的右准线于M,则线段PM的长为
上存在一点P使PF1⊥PF2,直线PF2交椭圆的右准线于M,则线段PM的长为
- A.2a
- B.2b
- C.2c
- D.

A
分析:利用椭圆的定义,PF1⊥PF2,可求PF1PF2=2b2,利用三角形PF1F2和三角形EMF2相似,可知 PF1=F2M,从而可求.
解答:由椭圆定义得PF1+PF2=2a,由PF1⊥PF2,F1F2=2c,
得(PF1)2+(PF2)2=4c2
所以(PF1+PF2)2=4a2,
即4c2+2PF1PF2=4a2,
即PF1PF2=2b2
设右准线与x轴交于E点,三角形PF1F2和三角形EMF2相似,
所以PF2F2M=F1F2FE=2c[ -c]=2b2=PF1PF2,
-c]=2b2=PF1PF2,
所以 PF1=F2M
∴PM=PF2+F2M=PF2+PF1=2a
故选A.
点评:本题以椭圆为载体,考查直线与椭圆的位置关系,考查椭圆的定义,有一定的综合性.
分析:利用椭圆的定义,PF1⊥PF2,可求PF1PF2=2b2,利用三角形PF1F2和三角形EMF2相似,可知 PF1=F2M,从而可求.
解答:由椭圆定义得PF1+PF2=2a,由PF1⊥PF2,F1F2=2c,
得(PF1)2+(PF2)2=4c2
所以(PF1+PF2)2=4a2,
即4c2+2PF1PF2=4a2,
即PF1PF2=2b2
设右准线与x轴交于E点,三角形PF1F2和三角形EMF2相似,
所以PF2F2M=F1F2FE=2c[
 -c]=2b2=PF1PF2,
-c]=2b2=PF1PF2,所以 PF1=F2M
∴PM=PF2+F2M=PF2+PF1=2a
故选A.
点评:本题以椭圆为载体,考查直线与椭圆的位置关系,考查椭圆的定义,有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
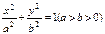 的离心率为
的离心率为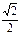 .
.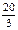 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程; 的值.
的值.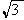 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求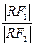 的值.
的值.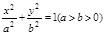 的离心率为
的离心率为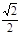 .
.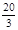 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;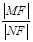 的值.
的值.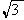 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求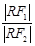 的值.
的值. 的离心率为
的离心率为 .
. 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆的方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆的方程;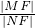 的值.
的值. y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求 的值.
的值.