题目内容
已知椭圆
 (
( )的离心率为
)的离心率为 ,
, 是椭圆的焦点,点
是椭圆的焦点,点 ,直线
,直线 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.

(1)求椭圆 的方程;
的方程;
(2)设过点 的直线与
的直线与 相交于
相交于 、
、 两点,当
两点,当 的面积最大时,求
的面积最大时,求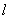 的方程.
的方程.
(1)设 ,由题意
,由题意 ,
,
∴ ,又∵离心率
,又∵离心率 ,∴
,∴ ,
,
∴ ,椭圆
,椭圆 的方程为
的方程为 ;
;

(2)由题意知,直线的斜率存在,设直线的斜率为 ,方程为
,方程为 ,
,
联立直线与椭圆方程: ,化简得:
,化简得: ,
,
由 ,∴
,∴ ,
,
设 ,则
,则  ,
,
∴ ,
,
坐标原点 到直线的距离为
到直线的距离为 ,
,
 ,
,
令 ,则
,则  ,
,
∵ ,当且仅当
,当且仅当 ,即
,即 时等号成立,
时等号成立,
∴ ,故当
,故当 , 即
, 即 ,
, ,
,
∴ 时
时 的面积最大,
的面积最大,
此时直线的方程为
考点:椭圆的定义、几何性质,直线与椭圆位置关系,基本不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, 满足|
满足| ,|
,| |=1,
|=1, •
• B.2 C.
B.2 C. (a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线交点坐标为(-2,-1),则双曲线的焦距为_______________.
(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线交点坐标为(-2,-1),则双曲线的焦距为_______________. :
:
 的右顶点为
的右顶点为
 为圆心的圆与双曲线
为圆心的圆与双曲线 的某渐近线交于两点
的某渐近线交于两点 .若
.若 且
且 ,则双曲线
,则双曲线

 B.
B. C.
C. D.
D.
 的图象上,以
的图象上,以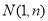 为切点的切线的倾斜角为
为切点的切线的倾斜角为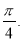
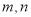 的值;
的值;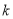 ,使得不等式
,使得不等式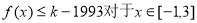 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数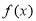 是定义域
是定义域 内的某个区间
内的某个区间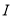 上的增函数,且
上的增函数,且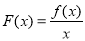 在
在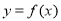 是I上的“非完美增函数”,已知
是I上的“非完美增函数”,已知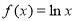 ,
,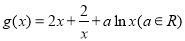 .
.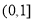 上是否是“非完美增函数”;
上是否是“非完美增函数”;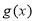 是
是 上的“非完美增函数”,求实数
上的“非完美增函数”,求实数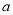 的取值范围.
的取值范围.