题目内容
已知极坐标系的原点在直角坐标系的原点处,极轴为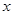 轴正半轴,直线
轴正半轴,直线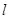 的参数方程为
的参数方程为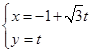 (
(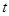 为参数),曲线
为参数),曲线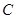 的极坐标方程为
的极坐标方程为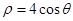 .
.
(1)写出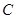 的直角坐标方程,并说明
的直角坐标方程,并说明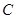 是什么曲线?
是什么曲线?
(2)设直线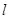 与曲线
与曲线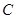 相交于
相交于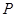 、
、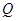 两点,求
两点,求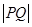 .
.
(1)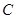 的直角坐标方程为
的直角坐标方程为 ,它表示圆心在
,它表示圆心在 ,半径为
,半径为 的圆;(2)
的圆;(2) .
.
解析试题分析:(1)掌握极坐标与直角坐标的互化公式即可解决问题;(2)将参数方程化为普通方程,运用直线与圆的位置关系知识即可解决此问题.
试题解析:(1)由
 ,所以
,所以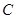 的直角坐标方程为
的直角坐标方程为 ,它表示圆心在
,它表示圆心在 ,半径为
,半径为 的圆. 5分
的圆. 5分
(2)将直线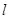 的参数方程为
的参数方程为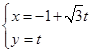 消去参数
消去参数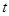 得普通方程
得普通方程 .
.
圆心 到直线
到直线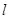 的距离
的距离 ,所以
,所以 . 10分
. 10分
考点:1.极坐标系与参数方程;2.直线与圆的位置关系.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
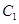 的方程为
的方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为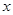 轴的正半轴建立平面坐标系,圆
轴的正半轴建立平面坐标系,圆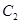 的参数方程
的参数方程 (
( 为参数),若圆
为参数),若圆 .
. (
( 为参数)与直线
为参数)与直线 (
( 为参数)垂直,则
为参数)垂直,则 .
.  的参数方程是
的参数方程是 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 ,则
,则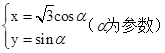 .
.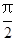 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;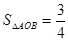 ;
; ,点P的轨迹为曲线C.
,点P的轨迹为曲线C. 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程; 距离的最大值.
距离的最大值. 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为: ,曲线C2的参数方程为:
,曲线C2的参数方程为: ,点N的极坐标为
,点N的极坐标为 .
. 的取值范围.
的取值范围.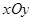 中,曲线
中,曲线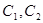 的参数方程分别为
的参数方程分别为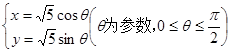 和
和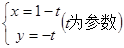 ,则曲线
,则曲线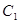 与
与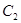 的交点坐标为
的交点坐标为  ,(t为参数),求直线的斜率.
,(t为参数),求直线的斜率.