题目内容
（2012•海淀区一模）已知三条侧棱两两垂直的正三棱锥的俯视图如图所示，那么此三棱锥的体积是2
| ||
| 3 |
2
| ||
| 3 |
| 2 |
| 2 |
分析：由题意可知，三条侧棱两两垂直的正三棱锥是正四面体，要求该三棱锥的体积和左视图的面积，必须求出正四面体的高及底面三角形的高，从而解决问题．
解答：
解：正三棱锥A-BCD的三条侧棱两两垂直，
∴正三棱锥A-BCD是正四面体，
底面是边长为2正三角形，底面上的高是
，
所以底面面积S=
×22=
，
A到底面的距离：h=
=
=
；
∴该三棱锥的体积V=
×
×
=
，
该三棱锥的左视图的面积：S△ADE=
×DE×AF=
×
×
=
故答案为：
；
．
解：正三棱锥A-BCD的三条侧棱两两垂直，∴正三棱锥A-BCD是正四面体，
底面是边长为2正三角形，底面上的高是
| 3 |
所以底面面积S=
| ||
| 4 |
| 3 |
A到底面的距离：h=
| AD2-DF2 |
22-(
|
2
| ||
| 3 |
∴该三棱锥的体积V=
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
该三棱锥的左视图的面积：S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
故答案为：
2
| ||
| 3 |
| 2 |
点评：本题考查三视图求面积，体积，空间想象能力，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
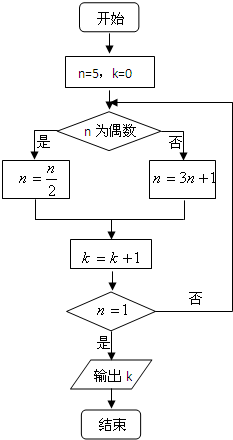（2012•海淀区一模）执行如图所示的程序框图，输出的k值是（ ）
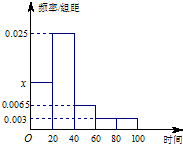（2012•海淀区一模）某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．