题目内容
两曲线y=x2+ax+b与2y=-1+xy3相切于点(1,-1)处,则a,b值分别为
- A.0,2
- B.1,-3
- C.-1,1
- D.-1,-1
D
分析:求出两个函数对x的导函数在切点(1,-1)的值,即两条曲线公切线的斜率,列出方程,求出a,将切点(1,-1)代入第一条曲线方程,求出b的值.
解答:对y=x2+ax+b关于x求导
y'=2x+a,y'|x=1=2+a
对2y=-1+xy3关于x求导
2y′=y3+3xy2y′解得y'=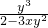 所以y'|x=1=
所以y'|x=1=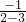 =1
=1
所以有2+a=1,解得a=-1
将点(1,-1)坐标代入y=x2+ax+b,有-1=1+a+b,
又a=-1,所以b=-2+1=-1
所以a=-1,b=-1
故选D
点评:本题考查求曲线的切线的问题时,一定要注意曲线的函数在切点处的值为切线的切线斜率.
分析:求出两个函数对x的导函数在切点(1,-1)的值,即两条曲线公切线的斜率,列出方程,求出a,将切点(1,-1)代入第一条曲线方程,求出b的值.
解答:对y=x2+ax+b关于x求导
y'=2x+a,y'|x=1=2+a
对2y=-1+xy3关于x求导
2y′=y3+3xy2y′解得y'=
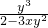 所以y'|x=1=
所以y'|x=1=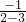 =1
=1所以有2+a=1,解得a=-1
将点(1,-1)坐标代入y=x2+ax+b,有-1=1+a+b,
又a=-1,所以b=-2+1=-1
所以a=-1,b=-1
故选D
点评:本题考查求曲线的切线的问题时,一定要注意曲线的函数在切点处的值为切线的切线斜率.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目