题目内容
已知函数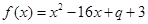 :
:
(1)若函数在区间 上存在零点,求实数
上存在零点,求实数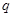 的取值范围;
的取值范围;
(2)问:是否存在常数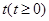 ,当
,当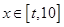 时,
时,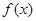 的值域为区间
的值域为区间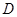 ,且
,且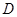 的长度为
的长度为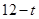 .
.
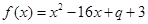 :
:(1)若函数在区间
 上存在零点,求实数
上存在零点,求实数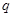 的取值范围;
的取值范围;(2)问:是否存在常数
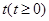 ,当
,当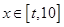 时,
时,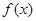 的值域为区间
的值域为区间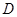 ,且
,且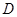 的长度为
的长度为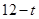 .
.(1) 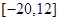 ;(2)存在,见解析.
;(2)存在,见解析.
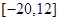 ;(2)存在,见解析.
;(2)存在,见解析.试题分析:(1) 先由函数对称轴为
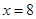 得函数在
得函数在 上单调减,要使函数在
上单调减,要使函数在 存在零点,则需满足
存在零点,则需满足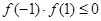 ,解得
,解得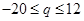 ; (2)当
; (2)当 时,
时,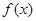 的值域为
的值域为 ,由
,由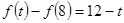 ,得
,得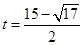 合题意;当
合题意;当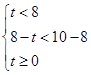 时,
时,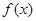 的值域为
的值域为 ,由
,由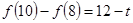 ,得不合题意;当
,得不合题意;当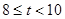 时,
时,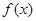 的值域为
的值域为 ,用上面的方法得
,用上面的方法得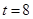 或
或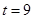 合题意.
合题意.试题解析:⑴ ∵二次函数
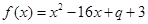 的对称轴是
的对称轴是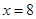
∴函数
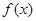 在区间
在区间 上单调递减
上单调递减∴要函数
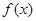 在区间
在区间 上存在零点须满足
上存在零点须满足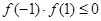
即
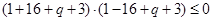
解得
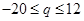 ,所以
,所以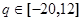 .
.⑵ 当
 时,即
时,即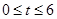 时,
时,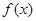 的值域为:
的值域为: ,即
,即 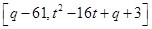
∴

∴
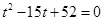 ∴
∴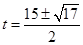
经检验
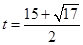 不合题意,舍去。
不合题意,舍去。当
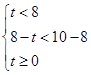 时,即
时,即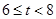 时,
时,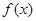 的值域为:
的值域为: ,即
,即 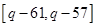
∴
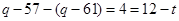 , ∴
, ∴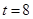
经检验
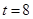 不合题意,舍去。
不合题意,舍去。当
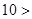
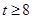 时,
时,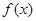 的值域为:
的值域为: ,即
,即 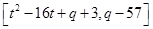
∴
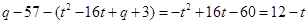
∴
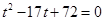 ∴
∴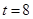 或
或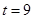
经检验
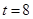 或
或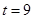 或
或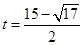 满足题意。
满足题意。所以存在常数
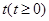 ,当
,当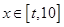 时,
时,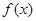 的值域为区间
的值域为区间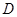 ,且
,且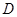 的长度为
的长度为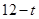 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
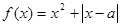 (
(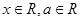 ).
).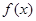 的奇偶性;
的奇偶性;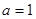 时,求
时,求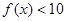 对
对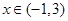 恒成立,求实数
恒成立,求实数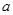 的取值范围.
的取值范围.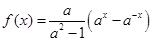 ,其中
,其中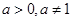
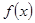 的奇偶性与单调性(不要求证明);
的奇偶性与单调性(不要求证明);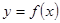 的定义域为
的定义域为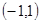 ,求满足不等式
,求满足不等式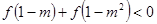 的实数
的实数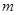 的取值集合;
的取值集合;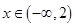 时,
时,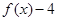 的值恒为负,求
的值恒为负,求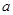 的取值范围.
的取值范围.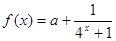 是奇函数.
是奇函数.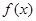 的单调性并证明;
的单调性并证明;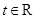 ,不等式
,不等式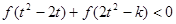 恒成立,求
恒成立,求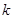 的取值范围.
的取值范围.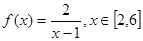 ,试判断此函数
,试判断此函数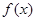 在
在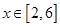 上的单调性,并求此函数
上的单调性,并求此函数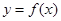 是R上的偶函数,且在区间
是R上的偶函数,且在区间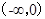 是单调递增的,若
是单调递增的,若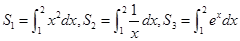 则下列不等式中一定成立的是( )
则下列不等式中一定成立的是( )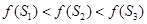
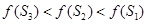
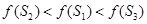
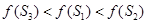
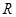 上的奇函数
上的奇函数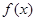 ,满足
,满足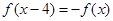 ,且在区间
,且在区间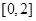 上是增函数,则( ).
上是增函数,则( ). 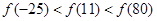
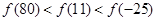
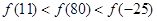
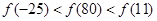
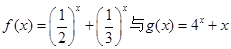 的交点的横坐标为
的交点的横坐标为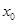 ,当
,当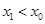 时
时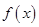
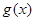 (从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)
(从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上) )上是增函数的是
)上是增函数的是


