题目内容
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1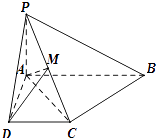
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
【答案】
(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
∴AB∥CD,
又AB平面PCD,CD平面PCD,
∴AB∥平面PCD
(2)∵∠ABC=45°,CB= ![]() ,AB=2,
,AB=2,
∴AC2=AB2+BC2﹣2ABBCcos45°= ![]() =2.
=2.
则AC2+BC2=AB2,∴BC⊥AC.
∵PA⊥平面ABCD,BC平面ABCD,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,
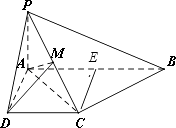
则四边形ADCE为矩形,∴AE=DC,AD=EC.
在Rt△CEB中,可得BE=BCcos45°= ![]() ,
,
CE=BCsin45°= ![]() ,∴AE=AB﹣BE=2﹣1=1
,∴AE=AB﹣BE=2﹣1=1
∴S△ADC= ![]() =
= ![]() =
= ![]() .,
.,
∵M是PC的中点,∴M到平面ADC的距离是P到平面ADC距离的一半,
∴VC﹣MAD=VM﹣ACD= ![]() ×S△ACD×(
×S△ACD×( ![]() PA)=
PA)= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)利用线面平行的判定定理证明;(2)利用勾股定理证明BC⊥AC,由PA⊥平面ABCD,可得PA⊥BC.从而可证得BC⊥平面PAC:(3)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,AE=DC,AD=EC.求得CE,计算△ACD的面积,根据M到平面ADC的距离是P到平面ADC距离的一半,求得棱锥的高,代入体积公式计算.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目