Question

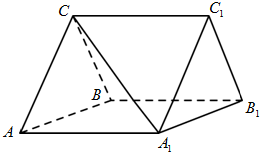如图，三棱柱ABC-A₁B₁C₁中，CA=CB，AB=AA₁，∠BAA₁=60°．
（Ⅰ）证明AB⊥A₁C；
（Ⅱ）若平面ABC⊥平面AA₁B₁B，AB=CB，求直线A₁C与平面BB₁C₁C所成角的正弦值．

Answer 1

分析：（Ⅰ）取AB的中点O，连接OC，OA₁，A₁B，由已知可证OA₁⊥AB，AB⊥平面OA₁C，进而可得AB⊥A₁C；
（Ⅱ）易证OA，OA₁，OC两两垂直．以O为坐标原点，

OA

的方向为x轴的正向，|

OA

|为单位长，建立坐标系，可得

BC

，

BB1

，

A1C

的坐标，设

n

=（x，y，z）为平面BB₁C₁C的法向量，则

n • BC =0 n • BB1 =0

，可解得

n

=（

3

，1，-1），可求cos＜

n

，

A1C

＞，即为所求正弦值．

解答：解：（Ⅰ）取AB的中点O，连接OC，OA₁，A₁B，
因为CA=CB，所以OC⊥AB，由于AB=AA₁，∠BAA₁=60°，
所以△AA₁B为等边三角形，所以OA₁⊥AB，
又因为OC∩OA₁=O，所以AB⊥平面OA₁C，
又A₁C?平面OA₁C，故AB⊥A₁C；
（Ⅱ）由（Ⅰ）知OC⊥AB，OA₁⊥AB，又平面ABC⊥平面AA₁B₁B，交线为AB，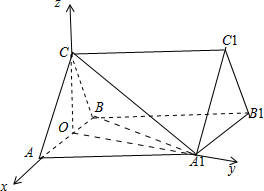
所以OC⊥平面AA₁B₁B，故OA，OA₁，OC两两垂直．
以O为坐标原点，

OA

的方向为x轴的正向，|

OA

|为单位长，建立如图所示的坐标系，
可得A（1，0，0），A₁（0，

3

，0），C（0，0，

3

），B（-1，0，0），
则

BC

=（1，0，

3

），

BB1

=

AA1

=（-1，

3

，0），

A1C

=（0，-

3

，

3

），
设

n

=（x，y，z）为平面BB₁C₁C的法向量，则

n • BC =0 n • BB1 =0

，即

x+ 3 z=0 -x+ 3 y=0

，
可取y=1，可得

n

=（

3

，1，-1），故cos＜

n

，

A1C

＞=

n • A1C

| n || A1C |

=-

10

5

，
故直线A₁C与平面BB₁C₁C所成角的正弦值为：

10

5

．

点评：本题考查直线与平面所成的角，涉及直线与平面垂直的性质和平面与平面垂直的判定，属难题．