题目内容

在平行六面体ABCD—A1B1C1D1中,已知对角线A1C=4,BD1=2,若空间一点P使PA1=3,PC=5,则PB2+PD12=_____________.

解析：在平行六面体AC1中,由于各侧面及底面均是平行四边形,可以推出A1D1BC.因此,四边形A1BCD1是平行四边形,其对角线A1C、BD1相交于一点且被这点平分.设A1C∩BD1=O,则OB=OD1=1,A1O=2.在△A1CP中,由A1C=4,PA1=3,PC=5,得∠PA1C=90°.连结PO,则PO=.设∠POB=α,则∠POD1=180°-α.在△POB中, PB2=PO2+OB2-2PO·OBcosα=14-2PO·cosα.在△POD1中,PD12=PO2+OD12-2PO·OD1cos(180°-α)

=14+2PO·cosα,所以PB2+PD12=28.

答案：28

练习册系列答案
相关题目
如图，在平行六面体ABCD-A1B1C1D1中，O为AC与BD的交点，若
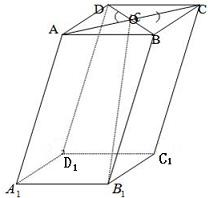
A1B1
=
a
，
A1D1
=
b
，
AA1
=
c
，则向量
B1O
等于（　　）
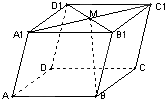精英家教网
A、
1
2
a
+
1
2
b
+
c
B、
1
2
a
-
1
2
b
+
c
C、-
1
2
a
+
1
2
b
+
c
D、-
1
2
a
-
1
2
b
+
c
精英家教网如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则下列向量中与
BM
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、-
1
2
a
-
1
2
b
+
c
D、
1
2
a-
1
2
b+c
在平行六面体ABCD-A1B1C1D1中，向量
D1A
、
D1C
、
A1C1
是（　　）
已知在平行六面体ABCD-A1B1C1D1中，AB=AD=AA1=1，且∠BAD=∠BAA1=∠DAA1=60°，求AC1的长．
在平行六面体ABCD-A1B1C1D1中，
AC
=
a
，
BD
=
b
，
AC1
=
c
，试用
a
、
b
、
c
表示
BD1
=
b
+
c
-
a
b
+
c
-
a
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网