题目内容

关于函数f（x）=4sin（2x+
π
3
），（x∈R）有下列命题：
①y=f（x）是以2π为最小正周期的周期函数；
②y=f（x）可 改写为y=4cos（2x-
π
6
）；
③y=f（x）的图象关于点（-
π
6
，0）对称；  
④y=f（x）的图象关于直线x=-
5π
12
对称；
其中正确的序号为______．
由题意可得函数的最小正周期为
2π
2
=π，故选项①错误；
由诱导公式可得f（x）=4sin（2x+
π
3
）=4cos[
π
2
-（2x+
π
3
））]
=4cos（
π
6
-2x）=4cos（2x-
π
6
），故选项②正确；
由2x+
π
3
=kπ，可得x=
k
2
π-
π
6
，k∈Z，当k=0时，x=-
π
6
，
故函数图象的一个对称点为（-
π
6
，0），故选项③正确；
由2x+
π
3
=kπ+
π
2
，可得x=
k
2
π+
π
12
，k∈Z，当k=-1时，x=-
5π
12
，
故函数图象的一条对称轴为x=-
5π
12
，故选项④正确．
故答案为：②③④
练习册系列答案
相关题目
关于函数f（x）=2（sinx-cosx）cosx的四个结论：
P1：最大值为
2
；
P2：最小正周期为π；
P3：单调递增区间为[kπ-
π
8
，kπ+
3
8
π]，k∈Z；
P4：图象的对称中心为(
k
2
π+
π
8
，-1)，k∈Z．
其中正确的有（　　）
关于函数f（x）=sin2x-cos2x有下列命题：
①函数y=f（x）的周期为π；                
②直线x=
π
4
是y=f（x）图象的一条对称轴；
③点(
π
8
，0)是y=f（x）图象的一个对称中心；
④(-
π
8
，
3π
8
)是函数y=f（x）的一个单调递减区间．
其中真命题的序号是
①③
①③
．
（2008•盐城一模）给出定义：若m-
1
2
＜x≤m+
1
2
（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即 {x}=m．在此基础上给出下列关于函数f（x）=|x-{x}|的四个命题：
（1）y=f（x）的定义域是R，值域是[0，
1
2
]
（2）y=f（x）是周期函数，最小正周期是1
（3）y=f（x）的图象关于直线x=
k
2
（k∈Z）对称
（4）y=f（x）在[-
1
2
，
1
2
]上是增函数   
则其中真命题是
（1）、（2）、（3）
（1）、（2）、（3）
．
已知下表为函数f（x）=ax3+cx+d部分自变量取值及其对应函数值，为便于研究，相关函数值非整数值时，取值精确到0.01．
x 3.27 1.57 -0.61 -0.59 0.26 0.42 -0.35 -0.56 0 4.25
y -101.63 -10.04 0.07 0.026 0.21 0.20 -0.22 -0.03 0 -226.05
下列关于函数f（x）的叙述：
（1）f（x）为奇函数；                          （2）f（x）在[0.55，0.6]上必有零点
（3）f（x）在（-∞，-0.35]上单调递减；         （4）a＜0
其中所有正确命题的个数是（　　）

关于函数f（x）= 4 sin（2x+）（），有下列命题：

①由可得必是的整数倍；

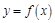②的表达式可改写为；

③的图象关于点对称；

④的图象关于直线对称．

其中正确命题的序号是________________．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网