题目内容
若曲线 上任意一点处的切线斜率恒为非负数,则b的取值范围是
上任意一点处的切线斜率恒为非负数,则b的取值范围是
- A.-2≤b≤2
- B.-2<b≤2
- C.-2≤b<2
- D.-2<b<2
A
分析:根据导数的几何意义求出函数f(x)在x=x0处的导数,从而求出切线的斜率,则x02+2bx0+4>0对?x0∈R恒成立,然后利用判别式进行求解即可.
解答:设点(x0,y0)为曲线 上的任意一点,
上的任意一点,
则该点处的切线斜率为k=y′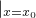 =x02+2bx0+4;
=x02+2bx0+4;
∴由已知得x02+2bx0+4≥0对?x0∈R恒成立;
∴△=4b2-16≤0,解得-2≤b≤2.
故选A.
点评:本题以函数为载体,考查导数的几何意义,同时考查了转化与划归的思想,属于基础题.
分析:根据导数的几何意义求出函数f(x)在x=x0处的导数,从而求出切线的斜率,则x02+2bx0+4>0对?x0∈R恒成立,然后利用判别式进行求解即可.
解答:设点(x0,y0)为曲线
 上的任意一点,
上的任意一点,则该点处的切线斜率为k=y′
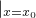 =x02+2bx0+4;
=x02+2bx0+4;∴由已知得x02+2bx0+4≥0对?x0∈R恒成立;
∴△=4b2-16≤0,解得-2≤b≤2.
故选A.
点评:本题以函数为载体,考查导数的几何意义,同时考查了转化与划归的思想,属于基础题.

练习册系列答案
相关题目
 满足:①当
满足:①当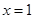 时有极值,②图象与y轴交点的纵坐标为
时有极值,②图象与y轴交点的纵坐标为 ,且在该点处的切线与直线
,且在该点处的切线与直线 垂直
垂直 的值域
的值域 上任意一点处的切线的斜率恒大于
上任意一点处的切线的斜率恒大于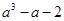 ,求
,求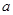 的取值范围
的取值范围 上任意一点处的切线的倾斜角都是锐角,那么整数
上任意一点处的切线的倾斜角都是锐角,那么整数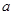 等于( )
等于( ) D
D
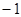
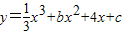 上任意一点处的切线斜率恒为非负数,则b的取值范围为 .
上任意一点处的切线斜率恒为非负数,则b的取值范围为 . 上任意一点处的切线斜率恒为非负数,则b的取值范围为 .
上任意一点处的切线斜率恒为非负数,则b的取值范围为 .