题目内容
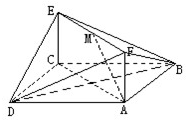 已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
(1)求证:AM∥平面BDE;
(2)求证:AM⊥平面BDF.
分析:(1)利用空间向量来证明,先建立空间直角坐标系,求出定点坐标,欲证AM∥平面BDE,只需用坐标证明向量
与平面BDE上的一个向量是平行向量即可.
(2)欲证AM⊥平面BDF,只需证明向量
与平面BDF中的两个不共线向量垂直即可,也即在平面BDF中找到两个向量,与向量
数量积等于0.
| AM |
(2)欲证AM⊥平面BDF,只需证明向量
| AM |
| AM |
解答: 解:建立如图的直角坐标系,则各点的坐标分别为:
解:建立如图的直角坐标系,则各点的坐标分别为:
O(0,0,0),A(0,1,0),B(-1,0,0),C(0,-1,0,),D(1,0,0,),
E(0,-1,1),F(0,1,1),M(0,0,1).
(1)∵
=(0,-1,1),
=(0,-1,1)
∴
=
,即AM∥OE,
又∵AM?平面BDE,OE?平面BDE,
∴AM∥平面BDE;
(2)∵
=(2,0,0),
=(-1,1,1),
∴
•
=0,
•
=0,
∴AM⊥BD,AM⊥DF,∴AM⊥平面BDF.
 解:建立如图的直角坐标系,则各点的坐标分别为:
解:建立如图的直角坐标系,则各点的坐标分别为:O(0,0,0),A(0,1,0),B(-1,0,0),C(0,-1,0,),D(1,0,0,),
E(0,-1,1),F(0,1,1),M(0,0,1).
(1)∵
| AM |
| OE |
∴
| AM |
| OE |
又∵AM?平面BDE,OE?平面BDE,
∴AM∥平面BDE;
(2)∵
| BD |
| DF |
∴
| AM |
| BD |
| AM |
| DF |
∴AM⊥BD,AM⊥DF,∴AM⊥平面BDF.
点评:本题主要考察了利用空间向量的平行或垂直证明立体几何中的线面平行,线面垂直.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
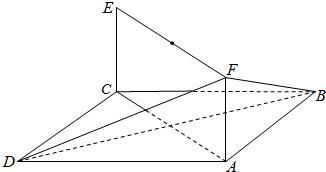 如图,已知正方形ABCD和矩形ACEF,EC⊥平面ABCD.AB=1,AF=1,
如图,已知正方形ABCD和矩形ACEF,EC⊥平面ABCD.AB=1,AF=1,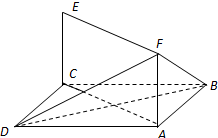 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直, 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=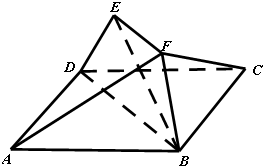 (2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,
(2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,