题目内容
已知椭圆 ,常数m、n∈R+,且m>n.
,常数m、n∈R+,且m>n.(1)当m=25,n=21时,过椭圆左焦点F的直线交椭圆于点P,与y轴交于点Q,若
 ,求直线PQ的斜率;
,求直线PQ的斜率;(2)过原点且斜率分别为k和-k(k≥1)的两条直线与椭圆
 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),试用k表示四边形ABCD的面积S;
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),试用k表示四边形ABCD的面积S;(3)求S的最大值.
【答案】分析:(1)求出椭圆的左焦点,设出P、Q坐标,利用若 ,和P在椭圆上,求出P、Q坐标,推出直线PQ的斜率;
,和P在椭圆上,求出P、Q坐标,推出直线PQ的斜率;
(2)写出直线l1:y=kx,l2:y=-kx与椭圆方程联立,求出A坐标,然后求出四边形ABCD的面积S;
(3)化简S的表达式, ,利用
,利用 的单调性,求出函数S的最大值.
的单调性,求出函数S的最大值.
解答:解:(1)∵m=25,n=21,∴ .(2分)
.(2分)
设满足题意的点为P(x,y)、Q(0,t). ,
,
∴(-2,-t)=2(x+2,y), .(4分)
.(4分)
 .(5分)
.(5分)
∴ .(6分)
.(6分)
(2)∵过原点且斜率分别为k和-k(k≥1)的直线l1:y=kx,l2:y=-kx关于x轴和y轴对称,
∴四边形ABCD是矩形.(8分)
设点A(x,y).
联立方程组 于是x是此方程的解,故
于是x是此方程的解,故 (10分)
(10分)
∴ .(12分)
.(12分)
(3) .
.
设 ,则g(k)在[1,+∞)上是单增函数.(13分)
,则g(k)在[1,+∞)上是单增函数.(13分)
理由:对任意两个实数k1、k2∈[1,+∞),且k1<k2,则
= =
= .(14分)
.(14分)
∵m>n>0,k2>k1≥1,∴k1k2>1,mk1k2-n>0.又k1-k2<0,
∴ .
.
∴g(k)在[1,+∞)上是单增函数,于是g(k)min=g(1)=m+n.(16分)
∴ .
.
∴ .(18分)
.(18分)
点评:本题考查直线的斜率,直线与圆锥曲线的综合问题,考查学生分析问题解决问题的能力,是难度较大题目.
 ,和P在椭圆上,求出P、Q坐标,推出直线PQ的斜率;
,和P在椭圆上,求出P、Q坐标,推出直线PQ的斜率;(2)写出直线l1:y=kx,l2:y=-kx与椭圆方程联立,求出A坐标,然后求出四边形ABCD的面积S;
(3)化简S的表达式,
 ,利用
,利用 的单调性,求出函数S的最大值.
的单调性,求出函数S的最大值.解答:解:(1)∵m=25,n=21,∴
 .(2分)
.(2分)设满足题意的点为P(x,y)、Q(0,t).
 ,
,∴(-2,-t)=2(x+2,y),
 .(4分)
.(4分) .(5分)
.(5分)∴
 .(6分)
.(6分)(2)∵过原点且斜率分别为k和-k(k≥1)的直线l1:y=kx,l2:y=-kx关于x轴和y轴对称,
∴四边形ABCD是矩形.(8分)
设点A(x,y).
联立方程组
 于是x是此方程的解,故
于是x是此方程的解,故 (10分)
(10分)∴
 .(12分)
.(12分)(3)
 .
.设
 ,则g(k)在[1,+∞)上是单增函数.(13分)
,则g(k)在[1,+∞)上是单增函数.(13分)理由:对任意两个实数k1、k2∈[1,+∞),且k1<k2,则

=
 =
= .(14分)
.(14分)∵m>n>0,k2>k1≥1,∴k1k2>1,mk1k2-n>0.又k1-k2<0,
∴
 .
.∴g(k)在[1,+∞)上是单增函数,于是g(k)min=g(1)=m+n.(16分)
∴
 .
.∴
 .(18分)
.(18分)点评:本题考查直线的斜率,直线与圆锥曲线的综合问题,考查学生分析问题解决问题的能力,是难度较大题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
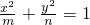 (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.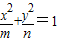 (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.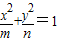 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..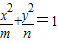 (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.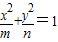 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值.. (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形. 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..