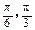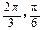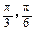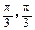题目内容
已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.

(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明: BD∥平面EFGH;
(3)设M是EG和FH的交点,
求证:对空间任一点O,有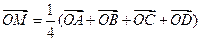 .
.

(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明: BD∥平面EFGH;
(3)设M是EG和FH的交点,
求证:对空间任一点O,有
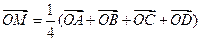 .
.证明略
(1)连结BG,则

由共面向量定理的推论知: E、F、G、H四点共面,(其中
 =
= )
)
(2)因为 .
.
所以EH∥BD,又EH 面EFGH,BD
面EFGH,BD 面EFGH
面EFGH
所以BD∥平面EFGH.
(3)连OM,OA,OB,OC,OD,OE,OG
由(2)知 ,同理
,同理 ,所以
,所以 ,EH
,EH FG,所以EG、FH交于一点M且被M平分,所以
FG,所以EG、FH交于一点M且被M平分,所以



由共面向量定理的推论知: E、F、G、H四点共面,(其中

 =
= )
)(2)因为
 .
.所以EH∥BD,又EH
 面EFGH,BD
面EFGH,BD 面EFGH
面EFGH所以BD∥平面EFGH.
(3)连OM,OA,OB,OC,OD,OE,OG
由(2)知
 ,同理
,同理 ,所以
,所以 ,EH
,EH FG,所以EG、FH交于一点M且被M平分,所以
FG,所以EG、FH交于一点M且被M平分,所以


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中, ,
, ,
, ,
,



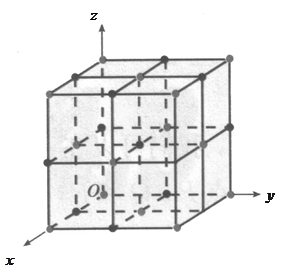
 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.如图(2),建立空间直角坐标
的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.如图(2),建立空间直角坐标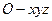 后,试写出全部钠原子所在位置的坐标.
后,试写出全部钠原子所在位置的坐标.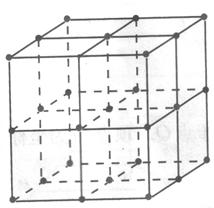
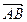 与
与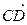 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
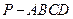 中,底面ABCD是一个平行四边形,
中,底面ABCD是一个平行四边形,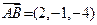 ,
,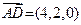 ,
,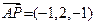
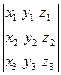 =
=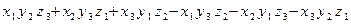 ,对于向量
,对于向量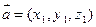 ,
,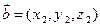 ,
,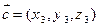 有
有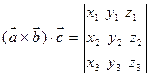 ,
,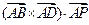 =__________.
=__________. =
=
 ,P是BN上的一点,若
,P是BN上的一点,若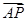 =m
=m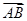 +
+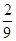
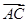 ,则实数m的值为( ).
,则实数m的值为( ).

 ·
· =1,则AB的长为 .
=1,则AB的长为 .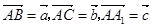 ,则
,则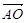 = ▲ .(试用
= ▲ .(试用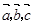 表示)
表示)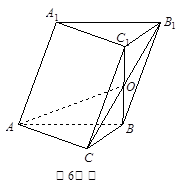
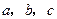 为
为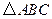 的三个内角
的三个内角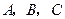 的对边,向量
的对边,向量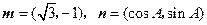 .若
.若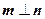 ,且
,且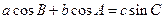 ,则角
,则角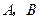 的大小分别为( )
的大小分别为( )