Question

若m∈（1，2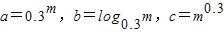），，则用“＞”将a，b，c按从大到小可排列为    ．

Answer 1

【答案】分析：由m∈（1，2），根据对数式的性质得到b=log_0.3m＜0，由指数函数的单调性得到0＜a＜1，c＞1，则a，b，c的大小可以比较．
解答：解：因为m∈（1，2），所以b=log_0.3m＜0，
0＜a=0.3^m＜0.3=1，
c=m^0.3＞m=1，
所以c＞a＞b．
故答案为c＞a＞b．
点评：本题考查了有理指数幂的化简与求值，考查了对数值的大小比较，解答此题的关键是明确指数函数的单调性，同时，对于log_ab，若a，b均大于0小于1，或均大于1，log_ab＞0；若a，b中一个大于0小于1，另一个大于1，则log_ab＜0，此题是基础题．