题目内容
(本小题满分14分)如图几何体, 是矩形,
是矩形, ,
,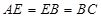 ,
,
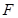 为
为 上的点,且
上的点,且 .
.

(1)求证: ;
;
(2)求证: .
.
 是矩形,
是矩形, ,
,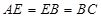 ,
,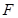 为
为 上的点,且
上的点,且 .
.
(1)求证:
 ;
;(2)求证:
 .
.(1)见解析(2)见解析
试题分析:(1)证明:

 ,
, .
.∴
 ,则
,则 ……………… (4分)
……………… (4分)又

 ,则
,则
∴
 . ……………………… (8分)
. ……………………… (8分)(2)证明:依题意可知:
 是
是 中点
中点
 则
则 ,而
,而 ,∴
,∴ 是
是 中点. (12分)
中点. (12分)在
 中,
中, ∴
∴ . ………………(14分)
. ………………(14分)点评:立体几何的证明计算还可用空间向量的方法解决,根据题目已知条件选择最合适的方法思路

练习册系列答案
相关题目
 中,
中, 平面
平面 ,
, ,
, ,
,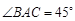 ,
, ,
, .
.
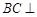 平面
平面
 和平面
和平面 所成角的正弦值
所成角的正弦值 的正切值;
的正切值;
 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( )









 是平面
是平面 内的两条不同直线,
内的两条不同直线, 是平面
是平面 内两条相交直线,则
内两条相交直线,则 的一个充分不必要条件是( )
的一个充分不必要条件是( )


