题目内容
如果两条曲线的方程是f1(x,y)=0和f2(x,y)=0,它们的交点是P(x0,y0),证明:方程f1(x,y)+λf2(x,y)=0的曲线也经过P点(λ∈R),并求经过两条曲线x2+y2+3x-y=0和3x2+3y2+y=0的交点的直线方程.
解析:∵P(x0,y0)是两曲线的交点,
∴f1(x0,y0)=0,f2(x0,y0)=0.
∴f1(x0,y0)+λf2(x0,y0)=0.
这就是说方程f1(x,y)+λf2(x,y)=0的曲线经过P.

①×3-②得
过两圆的交点的直线方程9x-4y=0.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程) 的图象不过原点,则m=1或m=2;
的图象不过原点,则m=1或m=2; =
= 表示经过点A(2,3)、B(-3,1)的直线;
表示经过点A(2,3)、B(-3,1)的直线;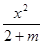 -
- =1表示的曲线不可能是椭圆;
=1表示的曲线不可能是椭圆;