题目内容
数列{an}对任意n∈N*，满足an+1=an+3，且a3=8，则S10等于
- A.155
- B.160
- C.172
- D.240
A
分析：由an+1=an+3，知{an}是公差d=3的等差数列，由a3=a1+2d=8，知a1=8-2d=8-6=2，由此能求出S10的值．
解答：∵an+1=an+3，
∴an+1-an=3，
∴{an}是公差d=3的等差数列，
∵a3=a1+2d=8，
∴a1=8-2d=8-6=2，
∴
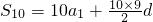
=10×2+5×9×3
=155．
故选A．
点评：本题考查等差数列的前n项和的计算，是基础题．解题时要认真审题，仔细解答．
分析：由an+1=an+3，知{an}是公差d=3的等差数列，由a3=a1+2d=8，知a1=8-2d=8-6=2，由此能求出S10的值．
解答：∵an+1=an+3，
∴an+1-an=3，
∴{an}是公差d=3的等差数列，
∵a3=a1+2d=8，
∴a1=8-2d=8-6=2，
∴
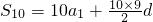
=10×2+5×9×3
=155．
故选A．
点评：本题考查等差数列的前n项和的计算，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目