Question

已知ab＞0，下面四个等式中：
①lg（ab）=lga+lgb； 
②； 
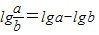③； 
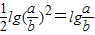④
其中正确命题的个数为（ ）
A．0
B．1
C．2
D．3

Answer 1

【答案】分析：直接通过对数的基本性质判断A、B、C的正误；通过对数的换底公式判断D的正误即可．
解答：解：对于①lg（ab）=lga+lgb，当a＞0、b＞0时成立，a＜0、b＜0时不成立，所以①不正确； 
对于②，当a＞0、b＞0时成立，a＜0、b＜0时不成立，所以②不正确； 
对于③，当＞0时成立，＜0时不成立，所以③不正确； 
对于④，因为=，满足换底公式，所以④正确．
故选B．
点评：本题考查对数的基本性质与换底公式的应用，命题的真假的判断，考查基本知识的应用．