题目内容
已知函数f(x)=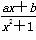 是定义在(-1,1)上的奇函数,且f
是定义在(-1,1)上的奇函数,且f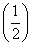 =
=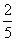 .
.
(1)确定函数f(x)的解析式;
(2)当x∈(-1,1)时判断函数f(x)的单调性,并证明;
(3)解不等式f(2x-1)+f(x)<0.
解析: (1)由题意可知f(-x)=-f(x),
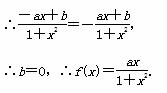 又∵f
又∵f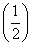 =
=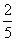 ,∴a=1,
,∴a=1,
∴f(x)=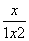 .
.
(2)当x∈(-1,1)时,函数f(x)是单调递增的.
证明如下:设任意的-1<x1<x2<1,
则f(x1)-f(x2)=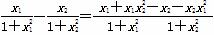
=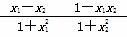 .
.
∵-1<x1<x2<1,
∴x1-x2<0,1-x1x2>0.
又1+x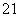 >0,1+x
>0,1+x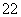 >0,
>0,
∴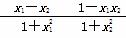 <0,
<0,
即f(x1)-f(x2)<0,∴函数f(x)为增函数.
(3)∵f(2x-1)+f(x)<0,
∴f(2x-1)<-f(x).
又f(x)是定义在(-1,1)上的奇函数,
∴f(2x-1)<f(-x),
∴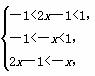 ∴0<x<
∴0<x<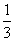 ,
,
∴不等式f(2x-1)+f(x)<0的解集为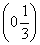 .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 若f(a)+f(-1)=2,则a=( )
若f(a)+f(-1)=2,则a=( )

